An inequality for polynomials with positives coefficients

Question

I have found in my old paper this theorem :

Let $a_i>0$ be real numbers and $x,y>0$ then we have : $$(x+y)f\Big(\frac{x^2+y^2}{x+y}\Big)(f(x)+f(y))\geq 2(xf(x)+yf(y))f\Big(\frac{x+y}{2}\Big)$$ Where :$$f(x)=\sum_{i=0}^{n}a_ix^i$$

The problem is I can't find the proof I made before . Furthermore I don't know if it's true but I have checked this inequality a week with Pari\Gp and random polynomials defined as before .

So first I just want a counter-examples if it exists .

If it's true if think it's a little bit hard to prove . I have tried the power series but without success . Finally it's a refinement of Jensen's inequality for polynomials with positives coefficients .

Thanks a lot if you have a hint or a counter-example .

Ps:I continue to check this and the equality case is to $x=y$

Answer 1

Even for $f(x)=x^n$ it's not so easy.

We need to prove $$(x+y)\Big(\frac{x^2+y^2}{x+y}\Big)^n(x^n+y^n)\geq 2\left(x^{n+1}+y^{n+1}\right)\Big(\frac{x+y}{2}\Big)^n$$ or $$2^{n-1}(x^2+y^2)^n(x^n+y^n)\geq\left(x^{n+1}+y^{n+1}\right)(x+y)^{2n-1}.$$ Now, let $x=ty$.

Also, since our inequality is symmetric, we can assume that $t\geq1.$

Thus, we need to prove that $g(t)\geq0,$ where $$g(t)=(n-1)\ln2+n\ln(t^2+1)+\ln(t^n+1)-\ln\left(t^{n+1}+1\right)-(2n-1)\ln(t+1).$$ Now, $$g'(t)=\frac{h(t)}{(t^2+1)\left(t^{n+1}+1\right)\left(t^n+1\right)(t+1)},$$ where $$h(t)=n(t-1)^3(t+1)t^{n-1}+2n(t-1)\left(t^{2n+1}+1\right)-(t^2+1)\left(t^{2n}-1\right).$$ Now, prove that $$h(1)=h'(1)=h''(1)=0$$ and $h'''(t)\geq0$ for all $t\geq1.$

Answer 2

Here is a partial answer. I show below that your inequality holds when $n\leq 5$.

Let $d=(x+y)^n\frac{LHS-RHS}{(y-x)^4}$. This turns out to be a polynomial, and a computation in PARI-GP (see below) reveals that $d$ is a polynomial in positive coefficients in $x,y,a_0,a_1,\ldots,a_n$ when $n\leq 4$ ; I call $d$ a completely positive polynomial.

Things become more complicated for $n=5$, because we have a "negative component" equal to

$$ -\frac{35}{16}a_0a_5(x^4y^3+x^3y^4) $$

However, we are still able to obtain positivity of $d$ in this case because the $a_0a_5$ coefficient is of the form $(y-x)^2$ times something completely positive.

As $n$ grows, the negative monomials grow in number too but they remain a minority, so the method for $n=5$ can probably be generalized.

Here is the PARI-GP code I used :

n0=4
aa(k)=eval(Str("a",k))
expr1=sum(j=0,n0,aa(j)*(u^j))
expr2=subst(expr1,u,p/q)*(q^n0)
expr3=subst(subst(expr2,p,x^2+y^2),q,x+y)
exprx=subst(expr1,u,x)
expry=subst(expr1,u,y)
main0=(x+y)*expr3*(exprx+expry)-\
2*((x+y)^n0)*(x*exprx+y*expry)*(subst(expr1,u,(x+y)/2))
main=main0/((y-x)^4)

Answer 3

I have tried many approaches to prove this inequality, but none worked. By now, I think that the inequality doesn't hold and thus I started to search for a counterexample. Michael Rozenberg has gave a proof for the special case $f(x) = x^n$ and Ewan Delanoy verifies this inequality for polynoms with degree at most $5$.

First we note that the condition that all $a_i >0$ are positive is unnecessary: If the inequality is valid for all $a_i> 0$, then we could let $a_i \downarrow 0$ for any index $i =0,\ldots,n$ and the inequality would remain to be valid.

However, it is in general wrong: Let $x=1$ and $y=t$ and take $f(x) = 1+x^{10}$. Then the function $$g(t):= (1+t) f \Big( \frac{t^2+1}{1+t} \Big)(f(1)+f(t)) - 2 (f(1)+t f(t)) f \Big( \frac{t+1}{2} \Big) $$ is negative for $t=0.5$: See this plot in WolframAlpha.

Conjecture: Is the inequality valid if we additionally require that $a_0 \ge a_1 \ge ... \ge a_n$?

I couldn't find any counterexample on this strengthened variant, but also no promising approach to prove this. Maybe someone has an idea?

Answer 4

A partial solution

Let $u=\frac{x}{x+y},v=\frac{y}{x+y}$. Then the inequality becomes $$f(ux+vy)(\frac{1}{2}f(x)+\frac{1}{2}f(y))\geq (uf(x)+vf(y))f\Big(\frac{x+y}{2}\Big)$$

In this form it is clear that the inequality depends upon the relative "importance" of two applications of Jensen's inequality.

Answer 5

Conjecture:

$$(x+y)f_n\Big(\frac{x^2+y^2}{x+y}\Big)(f_n(x)+f_n(y))- 2(xf_n(x)+yf_n(y))f_n\Big(\frac{x+y}{2}\Big) = \frac{(x-y)^4}{(x+y)^{n-1}}g_m(x,y)$$

with $g_m(x,y) \ge 0$ a polynomial.

Answer 6

$\color{green}{\textbf{UPDATED.}}$

Since $f'(x) \ge 0,$ then $f(x)$ is the non-decreasing function of $x.$

If $n=0,$ then the given inequality becames identity.

Since $$\dfrac{2(xf(x)+yf(y))}{(x+y)(f(x)+f(y))} = 1 + \dfrac{(x-y)(f(x)-f(y))}{(x+y)(f(x)+f(y))},\tag1$$

then the given inequality can be presented in the equivalent form of

$$f\left(\dfrac{x^2+y^2}{x+y}\right) \ge \left(1+\dfrac{(x-y)(f(x)-f(y))}{(x+y)(f(x)+f(y))}\right)f\left(\dfrac{x+y}2\right).\tag2$$

$\color{brown}{\textbf{Case 1.}\quad \mathbf{n>0,\quad a_0=0}.}$

---

$\textbf{Case 1.1.}\quad \mathbf{(x,y)\in [1,\infty)^2}.$

---

Denote $$g(x) = \dfrac1x f(x)\ \Rightarrow f(x)=xg(x),$$

then $$f(xy) = xy\, g(xy)\ge xy\,g(x) = y f(x),$$

$$2(x^2+y^2) = (x+y)^2+(x-y)^2,$$ $f\left(\dfrac{x^2+y^2}{x+y}\right) \ge \left(1+\dfrac{(x-y)^2}{(x+y)^2}\right)f\left(\dfrac{x+y}2\right).\tag3$

On the other hand, the inequality $$1+\dfrac{(x-y)^2}{(x+y)^2}\ge1 + \dfrac{(x-y)(f(x)-f(y))}{(x+y)(f(x)+f(y))},\tag4$$

or $$(x-y)^2(f(x)+f(y))\ge (x^2-y^2)(f(x)-f(y)),$$ $$2(x-y)(yf(x)-xf(y))\ge 0,$$ $$2xy(x-y)(g(x)-g(y))\ge 0,$$ is trivial for increasing $g(x).$

Multiplying of $(3)$ and $(4)$ leads to $(2).$

$\textbf{Case (1.1) is proved.}$

---

$\textbf{Case 1.2.}\quad \mathbf{m=\min(x,y) \in(0,1)}.$

---

Polynomial $f(x)$ can be presented in the form of $$f(x) = g(mx),$$ where $$g(u) = f\left(\dfrac um\right) = \sum\limits_{i=0}^n \dfrac{a_i}{m^i}\cdot u^i.$$

In accordance with the $\text{Case 1.1},\ \ g(u)$ satisfies to the given inequality if $(u,v)\in[1,\infty).$

$$(u+v)g\Big(\frac{u^2+v^2}{u+v}\Big)(g(u)+g(v))\geq 2(ug(u)+vg(v))g\Big(\frac{u+v}{2}\Big),$$

$$(u+v)f\Big(\frac 1m\frac{u^2+v^2}{u+v}\Big) \left(f\Big(\frac um\Big)+f\Big(\frac vm\Big)\right) \geq 2\left(uf\Big(\frac um\Big)+vf\Big(\frac um\Big)\right)f\Big(\frac{u+v}{2m}\Big),$$

$$\left(\Big(\frac um\Big)+\Big(\frac vm\Big)\right) f\left(\frac{\Big(\frac um\Big)^2+\Big(\frac vm\Big)^2}{\Big(\frac um\Big)+\Big(\frac vm\Big)}\right) \left(f\Big(\frac um\Big)+f\Big(\frac vm\Big)\right)\\ \geq 2\left(\Big(\frac um\Big)f\Big(\frac um\Big) +v\Big(\frac vm\Big)\Big(\frac vm\Big)\right) f\left(\frac{\Big(\frac um\Big)+\Big(\frac vm\Big)}{2}\right).$$

Therefore, $$(x+y)f\Big(\frac{x^2+y^2}{x+y}\Big)(f(x)+f(y))\geq 2(xf(x)+yf(y))f\Big(\frac{x+y}{2}\Big),$$ where $(x,y) \in[m,\infty).$

Since $m$ is an arbitrary real number, then $\textbf{Cases (1.2) and (1) are proved.}$

$\color{brown}{\text{Case 2.}\quad \mathbf{n>0,\quad a_0>0}.}$

In this case polynomial $f(x)$ can be presented as the production of the factors $(x+r_j)$ and $((x+p_k)^2+q_k^2).$

Denote $c = \min(r_j,p_k).$

---

$\textbf{Case 2.1.}\quad\mathbf{c\in\{r_k\}}.$

---

The polynomial $f(x)$ can be presented in the form of $$f(x) = (x+r)g(x+r),$$ wherein the polynomial $g(u)$ has positive coefficients.

If $r\in[1,\infty),$ then $$f(xy) = (x+r)(y+r) g((x+r)(y+r))\ge (x+r)yg((x+r)(y+r) = yf(x)),\tag5$$ and $\textbf{the further proof is similar to the Case 1.1}.$

If $r\in[0,1)$ and $(x,y)\in[1-r,\infty)^2,$ then $(5)$ is correct, and $\textbf{the further proof is similar to the Case 1.1}.$

If $r\in[0,1)$ and $(x,y)\in(0,1-r),$ then the polynomial $f(x)$ can be presented in the form of $$f(x) = \dfrac{x+r}r g\left(\dfrac{x+r}r\right),$$ wherein the polynomial $g(u)$ has positive coefficients.

Then $\textbf{the further proof is similar to the Case 1.2}.$

---

$\textbf{Case 2.2.}\quad\mathbf{c\in\{p_j\}.}$

---

The polynomial $f(x)$ can be presented in the form of $$f(x) = ((x+p)^2+q^2)g(x+p),$$ wherein the polynomial $g(u)$ have positive coefficients.

At the same time, $p$ can be negative.

For example, let us consider the polynomials in the form of $$f^\,_k(x) = 1+x^{4k+2} = (1+x^2)(1-x^2+x^4-\dots+x^{4k}).$$ If $k=1,$ then $4k+2=6,$ $$x^4-x^2+1 = (x^2+1)^2-3x^2 = (x^2-\sqrt3\,x+1)(x^2+\sqrt3\,x+1)$$ $$=\left(x^2-2x\cos\dfrac\pi6+1\right)\left(x^2+2x\cos\dfrac\pi6+1\right)$$ $$=\left(\left(x-\cos\dfrac\pi6\right)^2+\sin^2\dfrac\pi6\right) \left(\left(x+\cos\dfrac\pi6\right)^2+\sin^2\dfrac\pi6\right)$$ Then $$f^\,_1(x)=(x^2-2zx+1)(1+x^2)(x^2+2zx+1) = (x^2-2zx+1)g^\,_1(x-z),$$ wherein $g^\,_1(u)$ is the polynomial with the positive coefficients. Easy to show that for $k\ge1$ $$f^\,_k(x)=(x^2-2zx+1)g^\,_k(x-z),\tag6$$ where $$z= \cos^2\dfrac\pi{4k+2}\tag7$$ and

$$g^\,_k(u)=\dfrac{1+(u+z)^{4k+2}}{1-z^2+u^2} = \prod\limits_{j=2}^k \left(\left(u+z-\cos\dfrac{2j-1}{4k+2}\pi\right)^2+\sin^2 \dfrac{2j-1}{4k+2}\pi\right)$$ is the polynomial with the positive coefficients.

In particular, for $$x=\dfrac z2(1+d),\quad y=\dfrac z2(1-d)$$ one can get $$x+y = z,\quad x-y = zd,\quad x^2+y^2 = \dfrac{z^2}2(1+d^2),$$ $$f^\,_k\left(\dfrac z2(1+d^2)\right) - \left(1+d\dfrac{f^\,_k\left(\dfrac z2(1+d)\right)-f^\,_k\left(\dfrac z2(1-d)\right)} {f^\,_k\left(\dfrac z2(1+d)\right)+f^\,_k\left(\dfrac z2(1-d)\right)}\right)f^\,_k\left(\dfrac z2\right)$$ $$=\left(1+\left(\dfrac z2\right)^{4k+2}(1+d^2)^{4k+2}\right) - \left(1+d\cdot\dfrac{\left(\dfrac z2\right)^{4k+2}\left((1+d)^{4k+2}-(1-d)^{4k+2}\right)} {2+\left(\dfrac z2\right)^{4k+2}\left({\large\mathstrut}(1+d)^{4k+2}+(1-d)^{4k+2}\right)}\right)$$ $$=\left(\dfrac z2\right)^{4k+2}(1+d^2)^{4k+2}\left(1-\dfrac{d\left((1+d)^{4k+2}-(1-d)^{4k+2}\right)} {(1+d^2)^{4k+2}\left(2+\left(\dfrac z2\right)^{4k+2}\left({\large\mathstrut}(1+d)^{4k+2}+(1-d)^{4k+2}\right)\right)}\right)$$ $$\le \left(\dfrac z2\right)^{4k+2}(1+d^2)^{4k+2}\left(1-\dfrac{d\,(1+d)^{4k+2}} {(1+d^2)^{4k+2}\left(2+\left(\dfrac{1+d}2z\right)^{4k+2}\right)}\right),$$

and this allows to find counterexamples

• $k=2,\quad 4k+2=10,\quad (x,y) = \dfrac z2(1\pm d),\quad$ where$\quad z = \cos \dfrac\pi{10}\approx0.951,\quad d\in[0.328, 0.774]\quad$ (see also Wolfram Alpha calculations)

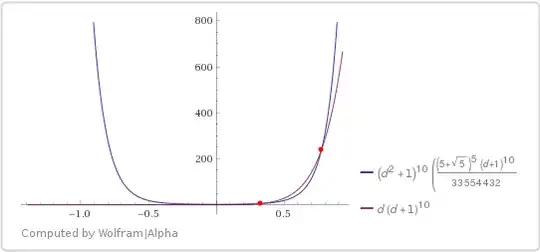
• $k=3,\quad 4k+2=14,\quad (x,y) = \dfrac z2(1\pm d),\quad$ where$\quad z = \cos \dfrac\pi{14}\approx0.975,\quad d\in[0.229, 0.856]\quad$ (see also Wolfram Alpha calculations)

• $k=4,\quad 4k+2=18,\quad (x,y) = \dfrac z2(1\pm d),\quad$ where$\quad z = \cos \dfrac\pi{10}\approx0.985,\quad d\in[0.181, 0.892]\quad$ (see also Wolfram Alpha calculations)

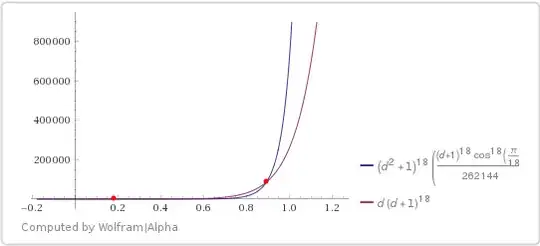
Therefore, in the case $(2.2)$ the given inequality $\color{brown}{\textbf{ allows counterexamples}}.$

Answer 7

First we rewrite your inequality as $$ \frac{\frac{1}{2}f(x) +\frac{1}{2}f(y)}{f\left(\frac{1}{2}x + \frac{1}{2}y\right)} \ge \frac{\frac{x}{x+y}f(x) +\frac{y}{x+y}f(y)}{f\left(\frac{x}{x+y}x + \frac{y}{x+y}y\right)}. $$ For $\lambda \in [0, 1]$, let $$ g(\lambda) = \frac{\lambda f(x) + (1 - \lambda) f(y)}{f(\lambda x + (1 - \lambda)y)}. $$ Since $f(x)$ is convex, we know $g(\lambda) \ge 1$. It suffice to show $g\left(\frac{x}{x+y}\right) \le g\left(\frac{1}{2}\right)$. Without losing generality, let's assume $x > y$. Furthermore, it suffice to show $g(\lambda)$ is a non-increasing function for $\lambda \in [\frac{1}{2}, \frac{x}{x+y}]$.

$$g^\prime(\lambda) = \frac{f(x) - f(y)}{f(\lambda x + (1 - \lambda)y)} - \frac{\lambda f(x) + (1 - \lambda) f(y)}{{\left(f(\lambda x + (1 - \lambda)y)\right)}^2}f^\prime(\lambda x + (1 - \lambda)y)(x-y).$$

For $g^\prime(\lambda)$, we are only concerned about its being positive or not. To simplify notation, we use $\stackrel{s}{=}$ to denote sign equality so that we can drop nonnegative terms.

We first consider the special case of $f(x)=x^n, n \ge 1$ (the case $n=0$ is trivial), then $ \frac{f^\prime(x)}{f(x)}=\frac{n}{x}.$ Hence $$ g^\prime(\lambda) = \frac{1}{{(\lambda x + (1 - \lambda)y)}^n}\left( {x^n - y^n} - n(x-y)\frac{\lambda x^n + (1-\lambda) y ^n}{\lambda x + (1 - \lambda)y} \right) \\ \stackrel{s}{=} (x^n - y^n)(\lambda x + (1 - \lambda)y) - n(x-y)\left(\lambda x^n + (1-\lambda) y ^n\right) \\ = (x^n - y^n)\left(\frac{x+y}{2}\right) - n(x-y)\left(\frac{x^n + y ^n}{2}\right) \quad\quad\text{(1)} \\ - (n-1)\left(\lambda - \frac{1}{2}\right)(x-y)(x^n - y ^n) \quad\quad\text{(2)}.$$

For $\lambda \in [\frac{1}{2}, \frac{x}{x+y}]$, it is easy to see (2) is non-positive. Note (1) is non-positive as well since $$ (x^n - y^n)\left(\frac{x+y}{2}\right) - n(x-y)\left(\frac{x^n + y ^n}{2}\right) \le 0 \\ \Longleftrightarrow (x^n - y^n)\left({x+y}\right) \le n(x-y)\left({x^n + y ^n}\right) \\ \Longleftrightarrow x^{n+1} - y^{n+1} -xy^n +yx^n \le n(x^{n+1}-y^{n+1}+xy^n-yx^n) \\ \Longleftrightarrow (n+1)\left(x^ny-xy^n\right) \le (n-1)\left(x^{n+1}-y^{n+1}\right) \\ \Longleftrightarrow (n+1)\left(z^n-z\right) \le (n-1)\left(z^{n+1}-1\right), z=\frac{x}{y}>1 \\ \Longleftrightarrow \ell(z) = (n-1)\left(z^{n+1}-1\right) - (n+1)\left(z^n-z\right) \ge 0. \text{ for } z>1 $$ The last statement is true since $\ell(1) = 0$ and $$\ell^\prime(z) = (n^2-1)z^n-(n+1)(nz^{n-1}-1)\\ = (n+1)\left(n(z^n-z^{n-1}) - (z^n - 1)\right)\\ = (n+1)(z-1)\left( nz^{n-1}-\sum_{i=0}^{n-1}z^i \right) \ge 0 \text{ for } z \ge 1.$$

For the case of $f(x)=x^n$, we have proven the inequality. I will try to generalize the conclusion to all polynomials with positive coefficients later when I get time.

---

Noticed that @p4sch put in a counter example for general polynomial cases, I will hence abandon any generalization efforts, and my proof is only valid for the special case of $f(x)=x^n$.

Answer 8

Edit: the proof is wrong in the last line, there is a counterexample to the statement in another answer.

I think I have a complete and easy to follow proof. First let's define some quantities: $S_k(x, y) = x^k + y^k$, $S^f_k(x, y) = S_k(f(x), f(y))$ and $T_f(x, y) = xf(x) + yf(y)$. Your inequality is trivial equivalent to: $$f\left(\frac{S_2}{S_1}\right) \frac{S_1^f}{S_0} \ge f\left(\frac{S_1}{S_0}\right) \frac{T_f}{S_1}$$

Now $f = \sum_i a_i x^i$: expanding the expression of $f$ in both sides, we are left with the inequality: $$\sum_{i,j} a_i \left(\frac{S_2}{S_1}\right)^i a_j \frac{S_j}{S_0} \ge \sum_{i,j} a_i \left(\frac{S_1}{S_0}\right)^i a_j \frac{S_{j+1}}{S_1}$$ Since $a_i, a_j > 0$ it is enough to prove that $\left(\frac{S_2}{S_1}\right)^i \frac{S_j}{S_0} \ge \left(\frac{S_1}{S_0}\right)^i \frac{S_{j+1}}{S_1}$. We will prove that $$\left(\frac{S_1^2}{S_2 S_0}\right)^i \le 1 \le \frac{S_1 S_j}{S_0 S_{j+1}}$$

For the LHS we have $S_1^2 = (x + y)^2 \le 2 (x^2 + y^2) = S_0 S_2 \Leftrightarrow 2xy \le x^2 + y^2$ which is true because of the square inequality, thus $\text{LHS} \le 1$.

For the RHS we must prove that $(x + y)(x^j + y^j) \ge 2 (x^{j+1} + y^{j+1})$ which as before is true if and only if $x^j y + y^j x \ge x^{j+1} + y^{j+1}$ and this is equivalent to the factorization $(x-y)(x^j - y^j) \le 0$ which is true for all choices of $x, y$ since the power operation preserves ordering.