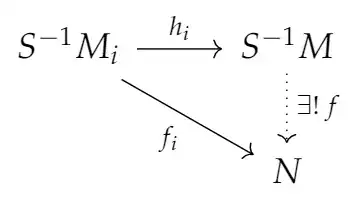Localization commutes with arbitrary direct sums

Question

Let $M_i$ be a arbitrary colection of $A$-modules and $S$ a multiplicative subset of $A$. I want to show that $$S^{-1}\left(\bigoplus_i M_i\right)\cong \bigoplus_i S^{-1}M_i$$ as $A$-modules and as $S^{-1}A$-modules. I know how to explicitly write an isomorphism between them but I want to do it using the universal properties to understand better how they work.

Here's what I've done:

Let $M=\bigoplus_i M_i$ with the canonical injections $\iota_i:M_i\to M$. Also let $\Phi:M\to S^{-1}M$ be the canonical morphism associated with the localization. Composing these morphisms we get $$\Phi\circ\iota_i:M_i\to S^{-1}M.$$ By the universal property of the localization, we obtain a unique morphism $$\overline{\Phi\circ\iota_i}:S^{-1}M_i\to S^{-1}M$$ such that $\overline{\Phi\circ\iota_i}\circ\Phi_i=\Phi\circ\iota_i$, where $\Phi_i:M_i\to S^{-1}M_i$ is the localization morphism.

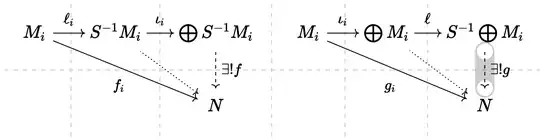
Finally, by the universal property of the coproduct we obtain a morphism $$\bigoplus_i S^{-1}M_i\to S^{-1}M.$$ I think this morphism might be the desired isomorphism but I don't know how to prove it.

(Maybe a good idea would be to find its inverse but for it I need some kind of morphism $M\to M_i$, which is not available when the direct sum is infinite.)

Also, I know there are a couple questions here about similar things but they do either the explicit isomorphism or the finite case.

Edit: after @GreginGre commentaries, I have a morphism $S^{-1}M\to S^{-1}M_i$ but I don't know neither how to obtain a morphism $S^{-1}M\to\bigoplus S^{-1}M_i$ (since this is the wrong side for the universal property of coproducts) nor how to show that these two morphisms are inverses of each other.

Answer 1

Might not be exactly what you want, but you only need to understand the following fact:

The localization $S^{-1}M$ is canonically isomorphic to the tensor product $S^{-1}A \otimes_A M$, as $S^{-1}A$-modules.

The question is then nothing but the fact that tensor product commutes with arbitrary direct sums (see e.g. this wiki page "distributive property").

Answer 2

Similarly as you have constructed the map, you can show that $\bigoplus_i S^{-1}M_i$ satisfies the universal property of $S^{-1}\bigoplus_i M$, which is just the combination of the universal property of localisation and the direct sum. This can be done 'by hand', which usually involves a large diagram, or as follows, if you are confident with functors:

We have the following sequence of natural equivalences of functors from the category of $S^{-1}A$-modules to the category of sets, given by various universal properties: $$\begin{align*} \hom_{S^{-1}A}(S^{-1}M,-) &= \hom_A(M,-|_A)\\ &=\prod\nolimits_i \hom_A(M_i,-|_A)\\ &=\prod\nolimits_i \hom_{S^{-1}A}(S^{-1}M_i,-|_A)\\ &= \hom_{S^{-1}A}\left(\bigoplus\nolimits_i S^{-1}M_i,-\right),\\ \end{align*}$$ where $-|_A$ means restriction of the $S^{-1}$-module structure to $A$.

This is the same as saying that their universal properties are equivalent; formally, one should invoke the Yoneda Lemma to conclude the claim. Tracing through the isomorphisms also tells you how to construct the isomorphisms if you plug in $S^{-1}M$ or $\bigoplus\nolimits_i S^{-1}M_i$ and look where the identity goes. And this shows that the map you've constructed is indeed the natural isomorphism.

Answer 3

I did (almost) what @Ben said and I think it worked well! It's not as pretty as working with functors, but it works for a beginner. I'll write here what I've done so it may help someone in the future.

Let $M=\bigoplus_i M_i$ be an arbitrary direct sum of $A$-modules with canonical injections $\iota_i:M_i\to M$. Composing with $\Phi:M\to S^{-1}M$ we get morphisms $M_i\to S^{-1}M$. By the universal property of localization, there are maps $h_i:S^{-1}M_i\to S^{-1}M$. These are the only maps such that $h_i\circ\Phi_i=\Phi\circ\iota_i$, where $\Phi_i:M_i\to S^{-1}M_i$ is the canonical map of the localization.

I affirm that $S^{-1}M$, along with these morphisms, satisfies the universal property of coproducts for $\bigoplus_i S^{-1}M_i$. Let $N$ be an $S^{-1}A$-module and $f_i:S^{-1}M_i\to N$ be morphisms. We want to show that there exists a unique morphism $f:S^{-1}M\to N$ such that the diagram

commutes.

Since $f_i\circ\Phi_i$ are morphisms from $M_i\to N$, we use the universal property of coproducts to obtain a morphism $\tilde{f}:M\to N$. Finally, by the universal property of localization, we obtain our morphism $f:S^{-1}M\to N$ which satisfies $f_i\circ\Phi_i=f\circ\Phi\circ\iota_i$. This means that $f_i\circ\Phi_i=f\circ h_i\circ\Phi_i$. By the uniqueness in the universal property of $S^{-1}M_i$, $f_i=f\circ h_i$ and so our diagram commutes. The uniqueness follows from the fact that we had unique morphisms all along the way.

Answer 4

I realize this probably will not be useful for the original poster, but I'm doing this exercise in Vakil right now and I think this explanation is worth having in mind. To make the use of universal properties explicit, we can "concatenate" the universal properties for coproducts and localization in two ways to form "two new universal properties": for any sequence of morphisms with common codomain $N$ (where $N$ satisfies the U.P. that it is an $S^{-1}A$ module), $(f_i:M_i\to N)_{i\in I}$, there are unique $f$ and $g$ satisfying the following commutative diagrams:

Then the claim is verified by replacing the first $N$ with $S^{-1}\bigoplus M_i$, and the second with $\bigoplus S^{-1}M_i$, and using the fact that these objects in the top right of each diagram are initial objects in some commma category (the objects are sequences of maps from the $M_i$, along with their common codomain, and the morphisms are maps from one codomain to another which make the natural triangular diagrams formed commute). It immediately follows by uniqueness of the maps to and from these initial objects that $f$ and $g$ are inverse isomorphisms (this was an earlier exercise in Vakil).