OTHER ANSWERS
To me the problem statement appeared to be simple and unambiguous, but what I first took from it did not lead me to the "right" answer.
For example the problem statement mentions "a block on level ground", but the solution that gives the "right" answer requires that it be suspended above ground.
Also the problem statements mentions that the end of the rope "is drawn directly away from the block and pulley at the rate
of 13 ft. per sec.". I thought that this meant that the rope is drawn at an angle that is at least approximately perpendicular to that of the rope hanging straight down from the pulley, and also that the length of the rope on the drawn side of the pulley was increasing in length at the rate given. Wrong. Or at least this meaning is not compatible with the "correct" solution.
All of which is to say that there are different reasonable interpretations of what is meant by the problem statement, and that which leads to the "right" answer is not necessarily the "best". I've already posted a solution that provides the "right" answer but it seemed wrong to not also mention other solutions I found that provided answers which were just as good, or better, than that given by the book. Hence this post.
Here again is the problem statement.
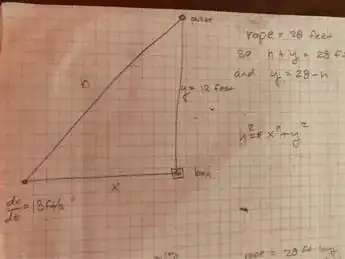
"A rope 28 feet long is attached to a block on level ground and runs
over a pulley 12 feet above the ground. The rope is stretched taut and
the free end is drawn directly away from the block and pulley at the rate
of 13 ft. per sec. How fast will the block be moving when it is 5 feet away
from the point directly below the pulley?"
HANGING BLOCK, CLOCKED PULLER
This is the solution which gives the "right" answer matching that found in the 3rd edition of the book (there was a different answer for the same problem in previous editions). I've already posted it at link below.
[''Correct'' Answer][https://math.stackexchange.com/a/4342106/1000346].
HANGING BLOCK, CLOCKED PULL
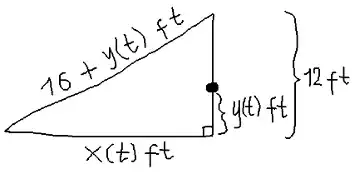
This solution is based on an interpretation of the problem statement which among other things has as given that block mentioned is no longer on level ground but is instead suspended with the point of attachment to the block being 5 feet above the point directly beneath the pulley, that the only pulley used is that which is mentioned, that speed of movement of the block (vertically) while suspended by the rope is what is to be found, and that the speed of pull on the rope or the rate at which it increases in length is given (rather than for example the speed of walking of the person pulling the rope).
Solving for rate of h
The rope is 28 feet long. It is one continuously connected rope but part of it is on one side of the pulley (attached to the block) and part of it is on the other side (being pulled). We'll label the rope on the block side of the pulley as $h$ and the part on the pulled side as $(28-h)$. The problem states that, "the free end is drawn directly away from the block and pulley at the rate of 13 ft. per sec", so it is given that $\frac{d(28-h)}{dt}=13$.
Because the rope is continuous it seems obvious that as the size of one side of the rope increases the size of the other side of the rope will decrease proportionally, so it is no surprise that:
$$\frac{d(28-h)}{dt}=13$$
$$\frac{d(28)-d(h)}{dt}=13$$
$$\frac{0-dh}{dt}=13$$
$$\frac{-dh}{dt}=13$$
$$\frac{dh}{dt}=-13$$
Solving for speed of block "when it is 5 feet away from the point directly below the pulley":
The block is suspended from the rope which runs over the pulley. Unless it is still swinging back and forth from being lifted up from the level ground it's only choice of movement is vertical, at the same rate. I'd call it movement along y because it is vertical, but again it's moving entirely with the movement of the rope which in this case forms not the hypotenuse but hangs directly from the pulley, so it's speed is also $\frac{dh}{dt}=-13$.
GROUNDED BLOCK, CLOCKED PULLER
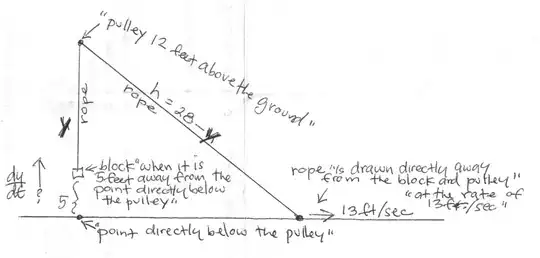
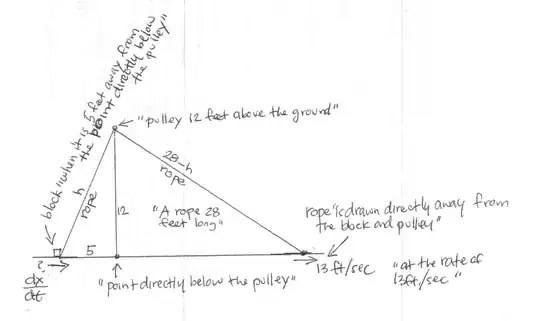This solution is based on an interpretation of the problem statement which among other things has as given that block mentioned is on level ground, that the only pulley used is that which is mentioned, that speed of movement of the block while still on level ground is what is to be found, and that the speed of pulling of the rope actually means the speed of walking of the person pulling the rope as measured horizontally. For this interpretation it does matter at what angle the rope is pulled and that it is 28 feet long. It is very similar to many two-cart problems I've found and the solution is the same as for those.
Solving for h
$$h^2=(x^2+12^2)=(5^2+12^2)=25+144=169$$
$$h=\sqrt 169=13$$
Solving for (28-h) and for y
$$(28-h)=(28-13)=15$$
$$15^2=(y^2+12^2)=(y^2+144)$$
$$y^2=(15^2-144)=225-144=81$$
$$y=\sqrt 81=9$$
Solving for rate of h
$$(28-h)^2=y^2+144$$
$$d[(28-h)^2]=d(y^2+144)$$
$$2(28-h)d(28-h)=2y\;dy$$
$$(28-h)(-dh)=y\;dy$$
$$(28-h)\frac{-dh}{dt}=y\;\frac{dy}{dt}$$
$$-15\;\frac{-dh}{dt}=9 \cdot 13$$
$$\frac{dh}{dt}=\frac{9 \cdot 13}{-15}=-\frac{39}{5}$$
Solving for rate of x
$$h^2=(x^2+12^2)=h^2=(x^2+144)$$
$$d[h*2)=d(x*2+144)$$
$$2h\;dh=2x\;dx$$
$$h\:\frac{dh}{dt}=x \frac{dx}{dt}$$
$$\frac{dx}{dt}=\frac{h \cdot \frac{dh}{dt}}{x}$$
$$\frac{dx}{dt}=\frac{13 \cdot -\frac{39}{5}}{5}$$
$$\frac{dx}{dt}=13 \cdot -\frac{39}{5} \cdot \frac{1}{5}$$
$$\frac{dx}{dt}=\frac{13(-39)}{25}$$
$$\frac{dx}{dt}=-\frac{507}{24}$$
$$\frac{dx}{dt}=-20.28 ft/sec$$
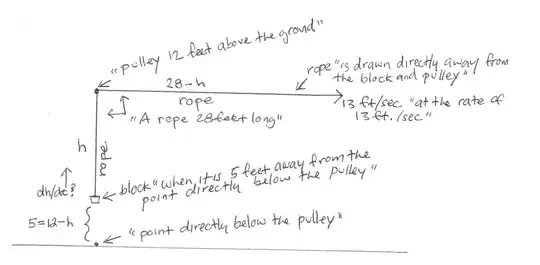
GROUNDED BLOCK, CLOCKED PULL
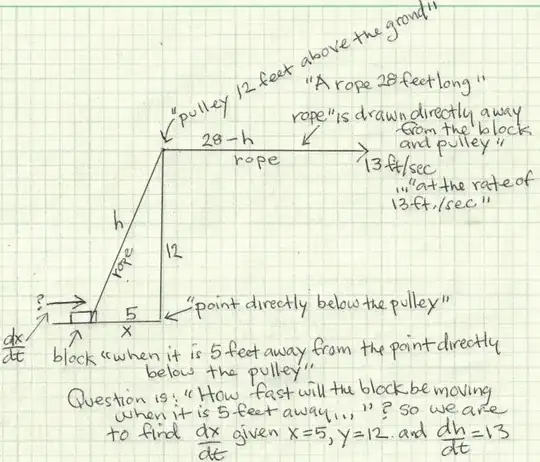
This solution is based on an interpretation of the problem statement which among other things has as given that block mentioned is on level ground, that the only pulley used is that which is mentioned, that speed of movement of the block while still on level ground is what is to be found, and that the speed of pulling of the rope is given (rather than for example the speed of walking of the person pulling the rope). For this interpretation it does not really matter at what exact angle the rope is pulled or even that it is 28 feet long.
Solving for h
$$h^2=(x^2+12^2)=(5^2+12^2)=25+144=169$$
$$h=\sqrt 169=13$$
Solving for rate of h
The rope is 28 feet long. It is one continuously connected rope but part of it is on one side of the pulley (attached to the block) and part of it is on the other side (being pulled). We'll label the rope on the block side of the pulley as $h$ and the part on the pulled side as $(28-h)$. The problem states that, "the free end is drawn directly away from the block and pulley at the rate of 13 ft. per sec", so it is given that $\frac{d(28-h)}{dt}=13$.
Because the rope is continuous it seems obvious that as the size of one side of the rope increases the size of the other side of the rope will decrease proportionally, so it is no surprise that:
$$\frac{d(28-h)}{dt}=13$$
$$\frac{d(28)-d(h)}{dt}=13$$
$$\frac{0-dh}{dt}=13$$
$$\frac{-dh}{dt}=13$$
$$\frac{dh}{dt}=-13$$
Solving for rate of x
Solving for horizontal speed of block "when it is 5 feet away from the point directly below the pulley":
$$h^2=x^2+12^2$$
$$x^2=h^2-12^2$$
$$d(x^2)=d(h^2-12^2)$$
$$2x \; dx=2h \; dh-0$$
$$x \; dx=h \; dh$$
$$x \; \frac{dx}{dt}=h \; \frac{dh}{dt}$$
$$\frac{dx}{dt}=h \; \frac{dh}{dt}\;\frac{1}{x}$$
$$\frac{dx}{dt}=13 \; (-13) \; \frac{1}{5}=-\frac{169}{5}$$
$$\frac{dx}{dt}=-33.8 \;(ft/sec)$$
Here is another try with a slightly different approach differentiating starting with $h$ rather than $h^2$:
$$\frac{hr}{dt}=-13 ft./sec$$
$$h^2=x^2+12^2=x^2+144$$
$$h=\sqrt(x^2+144)$$
$$dh=d[(x^2+144)^\frac{1}{2}]=\frac{d(x^2+144)}{2\sqrt(x^2+144)}$$
$$dh=\frac{2x\;dx+0}{2\sqrt(x^2+144)}=\frac{2x}{2\sqrt(x^2+144)}\;dx$$
$$dh=\frac{x}{\sqrt(x^2+144)}\;dx$$
$$\frac{dh}{dt}=\frac{x}{\sqrt(x^2+144)}\frac{dx}{dt}$$
$$\frac{dx}{dt}=\frac{\sqrt(x^2+144)}{x}\frac{dr}{dt}$$
$$\frac{dx}{dt}=\frac{\sqrt(5^2+144)}{5}(-13)=\frac{\sqrt(25+144)}{5}(-13)$$
$$\frac{dx}{dt}=\frac{\sqrt 169}{5}\;(-13)=\frac{13}{5}(-13)=-\frac{169}{5}$$
$$\frac{dx}{dt}=-33.8 ft./sec.$$
reality check
The answer above was surprising and led me to wonder if all my fancy calculations were blinding me to some obvious truth, so here's a low tech step-by-tiny-step example to verify this makes sense. Starting with the same given sizes what happens if we pull the 28 foot long rope a distance of only one sixteenth of an inch instead of 13 feet?
First the pulled end of the rope moves a distance of one sixteenth of an inch in the direction in which it is pulled (here "directly away from the block and pulley"). As the end of the rope where pulled moves one sixteenth of an inch so also does the part of the rope at the pulley, so that the part of the rope labeled $(28-h)$ becomes larger by one sixteenth of an inch, and the part of the rope labeled $h$ becomes smaller by one sixteenth of an inch.
At time t=0 seconds there are $(13 \times 12 \times 16=2496)$ sixteenth's of an inch in $h$,$(12 \times 12 \times 16=2304)$ sixteenth's of an inch from pulley to "the point directly below the pulley", and $(5 \times 12 \times 16=960)$ sixteenth's of an inch from the bottom of $h$ where it attaches to the block to "the point directly below the pulley").
At time t=1 second there are $(2496-1=2495)$ sixteenth's of an inch in $h$, $(12 \times 12 \times 16=2304)$ sixteenth's of an inch from pulley to "the point directly below the pulley", and $957.397$ sixteenth's of an inch from the bottom of $h$ where it attaches to the block to "the point directly below the pulley").
Summarizing
At t=0:
$$ x=960 $$
At t=1:
$$ h^2=x^2+2304^2$$
$$ 2495^2=x^2+2304^2$$
$$ x^2=2495^2-2304^2$$
$$ x=\sqrt (2495^2-2304^2)=957.397$$
Distance per second (in sixteenths of an inch):
$$ 960-957.397=2.603$$
At t=13:
$$ 13*2.603 = 33.839$$
The difference of one sixteenth of an inch in $h$ has resulted in a difference of 2.603 sixteenths of an inch in $x$. Therefore when $h$ is close to 13 feet long the rate at which $x$ contracts relative to $h$ is 2.603. If the rate at which $h$ is reduced is 13 feet/second then $x$ is reduced at the rate of $(13 \times 2.603=33.839)$ feet/second. The results from this numeric example is very close to that found using differentials above.
On a side note as to how this rate can be so surprisingly large notice that the 13 foot length of rope from the pulley to the block is very close to the end or terminal condition for pulling the block along the ground. At the rate of 13 feet/second it will be reduced in length to 12 foot and therefore stop pulling the block horizontally after only 1/13th of a second.
