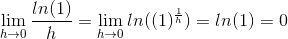0

when trying to prove the derivative i ended up with

$$\lim_{h \to 0}\frac{\ln(x+h)-\ln(x)}{h}=\lim_{h \to 0}\frac{\ln(\frac{x+h}{h})}{h}=\lim_{h \to 0}\ln((1+\frac{h}{x})^{(\frac{1}{h})}$$ and $$\frac{h}{x}\approx0$$ so

enter image description here

as you can see i attempted to solve it by treating $\frac{h}{x}$ as if its zero due to it being arbitrarily small but i got the wrong answer. now when trying to prove the derivative of $x^2$ i ended up with something similar:

$$\lim_{h \to 0}\frac{(x+h)^2-x^2}{h}=\lim_{h \to 0}\frac{x^2+h^2+2xh-x^2}{h}=\lim_{h \to 0}\frac{h^2+2xh}{h}=\lim_{h \to 0}h+2x=2x$$

here i treated h as if it were zero due to it being arbitrarily small and i got the right answer. was i wrong for treating $\frac{h}{x}$ as if its zero? (please forgive me for not writing the equations formally i am fairly new at this edit: when i was solving

crazyfoo
  • 55

3 Answers3

1

The first thing you missed was that $h$ was in the denominator such that you will get the power $\frac{1}{h}$ in the logarithm (which was fixed in the first line by an edit now and still is not fixed later on). Afterwards you let $h/x \rightarrow 0$ without considerung the $h$ in the power. You need to consider all the $h$'s at the same time when computing the limit. Here is how you can do it:

We have $$\lim_{h \rightarrow 0}\frac{\text{log}(x+h) - \text{log}(x)}{h} = \lim_{h \rightarrow 0}\text{log}\left(\left(1 + \frac{h}{x}\right)^{\frac{1}{h}}\right) = \lim_{h \rightarrow \infty}\text{log}\left(\left(1 + \frac{\frac{1}{x}}{h}\right)^{h}\right),$$ which is basically what you computed and using the continuity of the logarithm and the limit representation of the exponential function we now get $$\lim_{h \rightarrow \infty}\text{log}\left(\left(1 + \frac{\frac{1}{x}}{h}\right)^{h}\right)=\text{log}\left(\lim_{h \rightarrow \infty}\left(1 + \frac{\frac{1}{x}}{h}\right)^{h}\right) = \text{log}\left(\text{exp}\left(\frac{1}{x}\right)\right) = \frac{1}{x}.$$ Thus $\frac{d}{dx}\text{log}(x) = \frac{1}{x}$.

Con
  • 9,119
  • so your saying its wrong to treat h/x as zero? may i ask why though – crazyfoo Aug 25 '19 at 11:44
  • Well, I already told you. You are not computing the limit of $\frac{h}{x}$, but of $\left(1 + \frac{h}{x}\right)^{\frac{1}{h}}$. When the variable which is being used for the limit appears multiple times you cannot treat them seperately in general. I mean you could otherwise do things like $1 = \lim_{n \rightarrow \infty} 1 = \lim_{n \rightarrow \infty} \frac{n}{n} = \infty/0$ depending on which one you took for the computation. It is just not how you can compute limits. – Con Aug 25 '19 at 11:52
  • oh I didn't notice sorry, thanks for your help! – crazyfoo Aug 25 '19 at 11:58
  • No worries. Glad that I could help. Feel free to ask more. – Con Aug 25 '19 at 11:59
  • I now understand what you meant, but may I ask one more question. If I have a rational function for example x+5/x-8 and I take the limit of the function as x approaches zero I only need to consider the variable in denominator. So why is this situation different? – crazyfoo Aug 25 '19 at 13:21
  • No, you also need to consider both there. The way one computes that limit is the following: You can compute the limit for the enumerator and the denominator seperately at first which yields the limits $5$ and $-8$. Now if you have two converging sequences $(a_n){n \in \mathbb{N}}$ and $(b_n){n \in \mathbb{N}}$ with limits $a$ and $b$ respectively, then the sequence $(\frac{a_n}{b_n})_{n \in \mathbb{N}}$ converges to $\frac{a}{b}$ (we also need that only finitely many of the $b_n$ are zero). Thus applying that to your situation we get the limit $-\frac{5}{8}$. – Con Aug 25 '19 at 13:35
  • There are some rules that allow you to make computations easier by seperating some stuff, but you cannot do that always. – Con Aug 25 '19 at 13:36
0

$$\lim\limits_{h \to 0} \frac{\ln(x+h)-\ln(x)}{h} = \lim\limits_{h \to 0}\frac{1}{h} \ln\left(1+\frac{h}{x}\right) = \lim\limits_{h \to 0} \ln\left(1+\frac{h}{x} \right)^{\frac{1}{h}}$$

We use the limit formula: $$\lim\limits_{h \to 0}(1+a)^{\frac{1}{h}} = e^{\lim\limits_{h \to 0}\frac{a}{h}}$$

So our case we have $a =\frac{h}{x}$. Therefore let

$$\lim\limits_{h \to 0}\ln\left(1+\frac{h}{x} \right)^{\frac{1}{h}} = y$$ $$ \Rightarrow \lim\limits_{h \to 0}\left(1+\frac{h}{x} \right)^{\frac{1}{h}} = e^y \Rightarrow e^{\frac{1}{x}} = e^y \Rightarrow y =\frac{1}{x}$$

As required.

Rick
  • 1,099
0

$\lim\limits_{h\to0}\dfrac{\ln(x+h)-\ln x}{h}=\lim\limits_{h\to0}\dfrac{\ln\left(1+\dfrac hx\right)}h=\lim\limits_{h\to0}\dfrac{\dfrac hx+o(h)}h=\dfrac 1x$

J. W. Tanner
  • 63,683
  • 4
  • 43
  • 88