If $f(x)-f^{-1}(x)=e^{x}-1$, what is $f(x)$?

Question

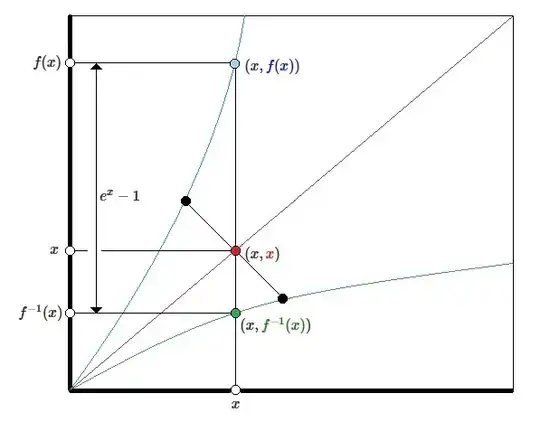
$f(x)$ is an increasing, differentiable function satisfying $f(x)-f^{-1}(x)=e^{x}-1$ for every real number $x$
I couldn't figure it out whether such function $f(x)$ exists or not.
And if it exists, I want to know the method to find what $f(x)$ is.
Thank you.

Answer 1

A general method for such problems is to use power series with undetermined coefficients. We decide to expand the function $f(x)$ as a power series around $x=0$. The equation to solve for $f$ is $$ f(x) - f^{-1}(x) = e^x-1. \tag1 $$ If $x=0$ then the right side is $0$ and thus $f(0)=f^{-1}(0).$ We are given that $f$ is increasing, thus $f(0)=0.$ Our Ansatz now becomes $$ f(x) = a_1 x + a_2 x^2 + a_3 x^3 + \cdots,\quad g(x) := f^{-1}(x) = b_1 x + b_2 x^2 + b_3 x^3 + \cdots. \tag2$$ We can find the power series for $g(x)$ using the Lagrange inversion theorem or by using the identity $f(g(x)) = x$ and solving for the coefficients of $g(x).$ By substituting equation $(2)$ into equation $(1)$ using the expansions of $f$ and $g$ we can solve for $a_1,a_2,a_3,\dots.$ The equation to solve for $a_1$ is $a_1-1/a_1=1$ whose positive solution is $a_1 = \phi := (1+\sqrt{5})/2.$ The rest of the coefficients are solutions of linear equations and the result is $$ f(x) = \phi\, x + \frac{\phi}4 x^2 + \frac{1+7\phi}{72} x^3 + \frac{13+170\phi}{6336} x^4 + \frac{-1279+5003\phi}{950400} x^5 + \cdots. \tag3 $$ There seems to be no obvious pattern to the coefficients. Of course, the radius of convergence is not yet known, and also if the power series is increasing. This is one of the limitations of this method. If the function has a power series, then we can find it, but we don't know much else about the function.

---

A general method which proves existence uses ideas from a solution to the Grossman's Constant problem. Specifically, the solution by Gabor Nyerges from 2000 in his "The Solution of the Functional Equation $x = (1+F(x))F^2(x)$" available from the Internet Archive Wayback Machine. His solution can be easily generalized to the functional equation $(1)$.

In more detail, consider the Fibonacci sequence $F_n$. The forward recurrence is $\,F_{n+2} = F_{n+1} + F_n\,$ for all integer $n.$ The backward recurrence is $\,F_{n-2} = F_n - F_{n-1}.\,$ There are two linearly independent solutions to the recurrence $\,u_{n+2} = u_{n+1} + u_n.\,$ One for each root of the characteristic polynomial $\,x^2 - x - 1.\,$ One root is the golden ratio $\,\phi := (1+\sqrt{5})/2 > 1\,$ the other is $\,0 > -1/\phi > -1.\,$ The solution for $\phi$ is exponentially increasing as $\,n \to \infty\,$ and also exponentially decreasing to $0$ as $n \to -\infty.\,$ The solution for the other root is exponentially alternating decreasing to $0$ as $\,n \to \infty\,$ and also exponentially alternating increasing as $\,n \to -\infty.\,$ Given two initial values $a_0$ and $a_1,$ the sequence is uniquely determined for all integer $n$ and is a linear combination of the two exponential solutions. As $\,n \to -\infty\,$ and if $\,u_0\,\phi = u_1,\,$ then $u_n$ decreases exponentially to $0,$ but if $\,u_0\,\phi \ne u_1,\,$ then the other solution is dominant and $u_n$ will eventually alternate in sign and become unbounded.

A similar situation arises in this question. Let us generalize the problem. Suppose that we want to construct $f(x)$ which is an increasing bijection on the reals that satisfies $$ f(x) - f^{-1}(x) = s(x) \tag{4} $$ where $\,s(x)\,$ is a differentiable function that satisfies $$ s(0) = 0 \quad \text{ and } \quad s'(x) > 0 \;\forall x. \tag{5} $$ Given $\,0 < x < y\,$ construct a sequence $\,u_n\,$ such that $$ u_0 = x,\quad u_1 = y,\quad u_{n+2} = s(u_{n+1}) + u_n\;\; \forall n\in\mathbb{Z}.\tag{6} $$ Notice that this is the Fibonacci recurrence if $\,s(x) = x.\,$ Notice that $\,u_{-1} = u_1 - s(u_0),\;\;$ $u_{-2} = u_0 - s(u_{-1}),\,$ and so on where we stop the backwards recursion if $\,u_n\,$ ever goes negative. Notice also that $\,u_{2k}\,$ and $\,u_{2k+1}\,$ are increasing sequences iff $\,u_n > 0\;\; \forall n \in\mathbb{Z},\,$ but the sequence $\,u_n\,$ itself may not be. We need to find out exactly when it is monotone increasing.

Now suppose that we know $\,s(x) = c_1\,x + O(x^2)\,$ where $\,c_1 > 1.\,$ By using arguments similar to the Fibonacci recurrence, we find that given $x$ there is a unique value of $\,y\,$ such that the sequence $\,u_n\,$ is such that $\,u_n \to 0\,$ monotonically as $\,n \to -\infty.\,$ Now define $\,f(x)\,$ to be this unique $\,y.\,$ This implies that $\, u_{n+1} = f(u_n)\;\; \forall n\in\mathbb{Z}.\,$ A similar argument holds for $\,x < 0\,$ using the forward recurrence. Thus $\,f(x)\,$ is defined for all reals. Because of equations $(5)$ and $(6)$ it is monotone increasing. Suppose that $\,s(x)\, > L > 0\,$ for $\,x > K > 0\,$ for some $\,L,K\,$ and the same with $>$ replaced with $<$. Then $\,f(x)\,$ is unbounded and hence it is a bijection. Standard $\delta-\epsilon$ methods can prove that $\,f(x)\,$ is differentiable.

Notice that similar arguments construct $\,f(x)\,$ if it is required to be a decreasing function instead of increasing. Notice that if $\,s(x) = c_1\,x\;\; \forall x\in\mathbb{R}\,$ then we have the linear recursion case and $\,f(x) = a_1\,x\,$ where $\,a_1\,$ is a positive root of the characteristic polynomial $\, x^2 - c_1\,x - 1.$

Answer 2

This is not an answer but only collects some properties which $f$ must neccesarily have.

Let us assume $f : \mathbb R \to \mathbb R$. Then

1. $f$ is a strictly increasing differentiable bijection.

2. $f'(x) > 0$ for all $x \in \mathbb R$. [Note that this does not follow from 1. as the example $f(x) = x^3$ shows.]

3. $f^{-1}$ is a strictly increasing differentiable bijection. We have $$(f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} > 0 .$$ Note that here it is essential to know that $f'$ does not have zeros.

4. One has the equation $$f'(x) - \frac{1}{f'(f^{-1}(x))} = e^x .$$

5. $f(0) = 0$.

6. $f'(0) = \frac{1+\sqrt{5}}{2} = \phi$, $(f^{-1})'(0) = \frac{1}{\phi} = \frac{-1+\sqrt{5}}{2}$.

7. $\lim_{x \to \infty}f'(x) = \infty$, $\lim_{x \to \infty}(f^{-1})'(x) = 0$.

8. If $\lim_{x \to -\infty}f'(x)$ exists, then it has the value $1$.

9. If $f$ has higher derivatives, we get additional functional equations. They can easily be computed recursively. Let us write $y = f^{-1}(x)$. Then the basic functional equation is $$f(x) - y = e^x -1 .$$ For $n > 0$ we get $$f^{(n)}(x) - y^{(n)} = e^x .$$ The $y^{(n)}$ can be computed recursively. We have $$y' = \frac{1}{f'(y)} ,$$ $$y'' = -\frac{f''(y) \cdot y'}{(f'(y))^2} = -\frac{f''(y)}{(f'(y))^3} ,$$ $$y''' = -\frac{f'''(y) \cdot y' \cdot (f'(y))^3 - f''(y)\cdot 3(f'(y))^2 \cdot f''(y) \cdot y'}{(f'(y))^6} \\ = - \frac{f'''(y) \cdot f'(y) - 3(f''(y))^2 }{(f'(y))^5}$$ etc. In this context see http://vixra.org/pdf/1703.0295v1.pdf which shows that there seems to exist no simple formula for $y^{(n)}$. Anyway, this allows to compute $f^{(n)}(0)$ and $(f^{-1})^{(n)}(0)$ recursively by noting that for $x= 0$ we have $y = 0$. This gives a linear equation for $f^{(n)}(0)$ whose solution can be expressed by the collection of $f^{(i)}(0)$ with $i < n$. Once we have determined the $f^{(i)}(0)$ with $i \le n$, we get $(f^{-1})^{(n)}(0)$ by inserting these values into the above equation for $y^{(n)}$. For example we get $$f''(0) = \frac{\phi^3}{1+\phi^3} = \frac{\phi}{2} , (f^{-1})''(0) = -\frac{\frac{\phi}{2}}{\phi^3} = -\frac{1}{2\phi^2} .$$

Let us give proofs.

1. In order to have an inverse $f^{-1}$ the function $f$ must be injective (in which case $f^{-1}$ is defined on $f(\mathbb R)$) and in order that $f(x) + f^{-1}(x)$ is defined for all $x \in \mathbb R$ the function $f$ must be surjective.

2. Since $f$ is increasing, we have $f'(x) \ge 0$ for all $x \in \mathbb R$. Replacing $x$ by $f(x)$ the functional equation yields $$f(f(x)) - x = f(f(x)) - f^{-1}(f(x)) = e^{f(x)} -1 .$$ Differentiating gives $$f'(x) \cdot f'(f(x)) - 1 = f'(x)\cdot e^{f(x)} .$$ This shows that $f'(x) \ne 0$ for all $x \in \mathbb R$.

3. $f^{-1}$ is trivially a bijection. Since $f'$ does not have zeros, it is differentiable with $(f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} > 0$. Hence $f^{-1}$ is increasing. Note that this also follows easily from the fact that $f$ is increasing (without using differentiabilty).

4. This is obtained by differentiating the functional equation.

5. We have $f(0) = f^{-1}(0)$. Assume $f(0) > 0$. Then $0 = f^{-1}(f(0)) > f^{-1}(0)$ which is impossible. Similarly $f(0) < 0$ is impossible.

6. By 4. $$f'(0) - \frac{1}{f'(0)} = f'(0) - \frac{1}{f'(f^{-1}(0))} = e^0 = 1 .$$ This implies (note $f'(0) > 0$) $f'(0) = \frac{1+\sqrt{5}}{2} = \phi$ and $(f^{-1})'(0) = \frac{1}{f'(0))} = \frac{1}{\phi}$.

7. This follows from $f'(x) = e^x + \frac{1}{f'(f^{-1}(x))}$ and 3.

8. We have $\lim_{x \to -\infty}(f'(x) - \frac{1}{f'(f^{-1}(x))}) = 0$. Assume that $a = \lim_{x \to -\infty}f'(x)$ exists, $0 \le a \le \infty$. Then also $\lim_{x \to -\infty}f'(f^{-1}(x)) = a$ since $f^{-1}$ is an increasing bijection. $a = 0$ is impossible since then $\lim_{x \to -\infty}(f'(x) - \frac{1}{f'(f^{-1}(x))}) = -\infty$. $a = \infty$ is impossible since then $\lim_{x \to -\infty}(f'(x) - \frac{1}{f'(f^{-1}(x))}) = \infty$. Hence $0 < a < \infty$ and $a - \frac{1}{a}= 0$ which yields $a= 1$.

Answer 3

If $f(x) = x+k (e^x-1)$, $0<k<1$, then $f^{-1}(x) = k+x-W(ke^{k+x})$, $W$ is the Lambert W function.

If $f(x)- f^{-1}(x)= e^x-1$, then $W(ke^{k+x})=k+(1-k)(e^x-1)$. Then plugging into $f^{-1}(x)$ gives $f^{-1}(x)= k+x-W(ke^{k+x})=k+x-(k+(1-k)(e^x-1))=x-(1-k)(e^x-1)$, which doesn't seem to be right because now $f^{-1}(f(x))\neq f(f^{-1}(x))\neq x$. I think a closed form for the solution is difficult to find, but maybe (?) you can choose a $k$, generate some points and interpolate. Good luck, my friend!

Answer 4

Calling $f_n(x) = \sum_{k=0}^n a_k x^k$ as an $n-$degree approximation we have

$$ f^{-1}(x) = f(x) -e^x+1 $$

or

$$ x = f\left(f(x)-e^x+1\right) $$

or putting the approximation

$$ x = f_n\left(f_n(x)-\sum_{j=1}^n\frac{x^j}{j!}\right) $$

now expanding and equating to zero the polynomial coefficients we have

$$ \left\{ \begin{array}{rcl} -a_1^2+a_1+1 &=&0\\ -a_2 a_1^2+a_2 a_1+\frac{a_1}{2}-a_2 &=&0\\ -a_3 a_1^3+3 a_3 a_1^2-2 a_2^2 a_1+a_2 a_1-4 a_3 a_1+\frac{a_1}{6}+2 a_2^2-a_2+a_3 &=&0\\ \vdots& = &0 \end{array} \right. $$

Attached a MATHEMATICA script to determine the polynomial coefficients

f[x_, n_] := Sum[Subscript[a, k] x^k, {k, 1, n}]
n = 5;
pol = x - f[f[x, n] - Sum[x^k/k!, {k, 1, n}], n];
coefs = Take[CoefficientList[pol, x], {2, n + 1}];
For[k = 1; sols = {}; j = 2, k <= n, k++,
  sol = Solve[(coefs[[k]] /. sols) == 0, Subscript[a,k]][[j]];
  j = 1;
  AppendTo[sols, sol];
  sols = Flatten[sols]
]
A = Table[Subscript[a, k], {k, 1, n}];
A /. sols

NOTE

For $n=2$ we have

$$ x-a_2 \left(a_2 x^2+a_1 x-\frac{x^2}{2}-x\right){}^2-a_1 \left(a_2 x^2+a_1 x-\frac{x^2}{2}-x\right)=0 $$

or

$$ 0\times 1+(1+a_1-a_1^2)x + (-a_2 a_1^2+a_2 a_1+\frac{a_1}{2}-a_2)x^2 + (-2 a_1 a_2^2+2 a_2^2+a_1 a_2-a_2)x^3+(-a_2^3+a_2^2-\frac{a_2}{4})x^4 \equiv 0 $$

but for $n=2$ we collect only the $n+1$ first coefficients which are

$$ \{0,1+a_1-a_1^2,-a_2 a_1^2+a_2 a_1+\frac{a_1}{2}-a_2\}= 0 $$

$$ f(x) = \frac{1}{2} \left(1+\sqrt{5}\right) x+\frac{1}{8} \left(1+\sqrt{5}\right) x^2+\frac{1}{144} \left(9+7 \sqrt{5}\right) x^3+\frac{\left(98+85 \sqrt{5}\right) x^4}{6336}+\frac{\left(2445+5003 \sqrt{5}\right) x^5}{1900800}+\frac{\left(18257 \sqrt{5}-2260\right) x^6}{30067200}+\frac{\left(192234608 \sqrt{5}-32376225\right) x^7}{1069610572800}+\frac{\left(15850653103 \sqrt{5}-45039491325\right) x^8}{650323228262400}+\cdots $$