The Fourier series $\sum_{n=1}^\infty (1/n)\cos nx$

Question

The series $$\sum_{n=1}^\infty \frac{\sin nx}{n}$$ is the Fourier series of the odd $2\pi$-periodic extension of $(\pi-x)/2, 0<x<\pi$.

My question is : $$\sum_{n=1}^\infty \frac{\cos nx}{n}$$ is the Fourier series of the even $2\pi$-periodic extension of what function?

Answer 1

The function $-\frac{1}{2}\ln(2-2\cos x)$ simplifies to $f(x)=-\ln(2\sin(x/2))$. We will show that the Fourier cosine series of $f(x), 0<x<\pi,$ is $$\sum_{n=1}^\infty \frac{\cos nx}{n}.$$ Firstly, $$\frac{1}{\pi}\int_0^\pi f(x)\,dx=\frac{1}{\pi}\int_0^\pi \ln 2+\ln(\sin(x/2))\,dx=0$$ because $$\int_0^\pi \ln(\sin(x/2)\,dx=2\int_0^{\pi/2}\ln(\sin(u))\,du=\int_0^\pi \ln(\sin(u))\,du=-\pi\ln 2$$ where the last equality can be found in Ahlfors' Complex Analysis p. 159. Let $n\ge 1$ be an integer. Using integration by parts with $u=\ln(\sin(x/2)$ and $dv=\cos(nx)\,dx$, and the fact that $\lim_{x\to 0^+}\sin(nx)\ln(\sin(x/2)=0$, we get (note that $\int_0^\pi \ln2\cos(nx)\,dx=0$) $$\int_0^\pi f(x)\cos nx\,dx=\frac{1}{2n}\int_0^\pi \cot(x/2)\sin nx\,dx=\frac{\pi}{2n}$$ where the last equality is from here. This proves that $$\frac{2}{\pi}\int_0^\pi f(x)\cos nx\,dx=\frac{1}{n}.$$

Note that the even $2\pi$-periodic extension of $-\ln(2\sin(x/2)), 0<x<\pi$ is the $2\pi$-periodic function $$-\ln\left|2\sin\left(\frac{x}{2}\right)\right|=\ln\left| \frac{1}{2}\csc\left(\frac{x}{2}\right)\right|,$$ $-\infty<x<\infty$.

Answer 2

The series can also be summed by more elementary methods, in addition to the ones already presented.

Write $$\sum_{n=1}^{\infty} \frac{e^{inx}}{n}$$ and note that this converges for all $x\neq 2k\pi, k\in\mathbb{Z}$. This is in fact the Taylor series of the principle branch of the complex logarithm albeit in disguise: $$\sum_{n=1}^{\infty} \frac{e^{inx}}{n}=-\log(1-e^{ix})=-\log|1-e^{ix}|-i \arg(1-e^{ix})$$

Now observe that $$|1-e^{ix}|=|e^{ix/2}|\cdot|\frac{e^{-ix/2}-e^{ix/2}}{2i}|\cdot|2i|=|-2\sin\frac{x}{2}|$$ and take the real part of the sum to get the answer.

With the aid of elementary geometry, the imaginary part yields the value the asker mentioned. Notice that $\{1-e^{ix}| x\in[0,2\pi]\}$ is a circle centered at 1. For a fixed $x\neq 0,\pi$, consider the triangle formed by $0$,$1$, and $1-e^{ix}$ and the answer follows after some care about the orientations of the angles.

Answer 3

The proof proposed by Winther is the method Euler used to derive $$ \sum_{n=1}^{\infty}\frac{\sin nx}{n}=\frac{\pi-x}{2}\quad (0<x<2\pi). $$ This is often called the first Fourier series, since Euler mentioned it in a letter to Christian Goldbach as early as 1744. He published his proof only ten years later. Euler's derivation can be justified by integrating partial sums instead of infinite series, and this works also for the cosine series:
Integrate the identity $$ \sum_{n=1}^N \sin nx = \frac{\cos \frac{x}{2}-\cos(N+\frac{1}{2})x}{2\sin \frac{x}{2}} $$ from $\pi$ to $x\in(0,2\pi)$ to get $$ \begin{split}\sum_{n=1}^N\frac{\cos nx}{n}&=\sum_{n=1}^N\frac{(-1)^n}{n}-\int_{\pi}^x\frac{\cos\frac{t}{2}-\cos(N+\frac{1}{2})t} {2\sin\frac{t}{2}}\mathrm{d}t\\ &=\sum_{n=1}^N\frac{(-1)^n}{n}-\log(\sin\frac{x}{2})+\int_{\pi}^x \frac{\cos(N+\frac{1}{2})t} {2\sin\frac{t}{2}}\mathrm{d}t. \end{split} $$ The integral approches 0 for $N\to\infty$ (follows immediately from integrating by parts). We thus get $$ \sum_{n=1}^{\infty}\frac{\cos nx}{n}=-\log 2-\log(\sin\frac{x}{2}) \quad (0<x<2\pi). $$ (The identity we start from can be derived without using the complex geometric series by adding up
$\cos(n-\frac{1}{2})x-\cos(n+\frac{1}{2})x=2\sin nx\,\sin\frac{x}{2} \ (1\leq n\leq N)$.)

Answer 4

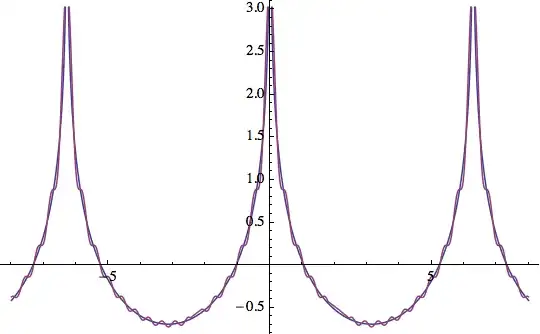
It seems to have escaped attention that this sum may be evaluated using harmonic summation techniques which can be an instructive exercise and usually succeeds on Fourier series. Here is an opportunity to contribute to an interesting, diverse and visually appealing series of posts.

Introduce $S(x)%$ given by $$S(x) = \sum_{n\ge 1} \frac{1}{n}\cos(nx).$$

The sum term is harmonic and may be evaluated by inverting its Mellin transform.

Recall the harmonic sum identity $$\mathfrak{M}\left(\sum_{k\ge 1} \lambda_k g(\mu_k x);s\right) = \left(\sum_{k\ge 1} \frac{\lambda_k}{\mu_k^s} \right) g^*(s)$$ where $g^*(s)$ is the Mellin transform of $g(x).$

In the present case we have $$\lambda_k = \frac{1}{k}, \quad \mu_k = k \quad \text{and} \quad g(x) = \cos(x).$$ We need the Mellin transform $g^*(s)$ of $g(x)$.

Now the Mellin transform of $\cos(x)$ was computed at this MSE link and found to be $$\Gamma(s) \cos(\pi s/2)$$

It follows that the Mellin transform $Q(s)$ of the harmonic sum $S(x)$ is given by

$$Q(s) = \Gamma(s)\cos(\pi s/2) \zeta(s+1) \quad\text{because}\quad \sum_{k\ge 1} \frac{\lambda_k}{\mu_k^s} = \sum_{k\ge 1} \frac{1}{k} \frac{1}{k^s} = \zeta(s+1)$$ for $\Re(s) > 0.$

The Mellin inversion integral here is $$\frac{1}{2\pi i} \int_{1/2-i\infty}^{1/2+i\infty} Q(s)/x^s ds$$ which we evaluate by shifting it to the left for an expansion about zero.

The zeros of the cosine term at the negative odd integers cancel the poles of the gamma function at those values. No additional cancelation is gained from the trivial zeros of the zeta function term $\zeta(s+1)$ as these are (also) at the odd negative integers to the left of $-1.$ This leaves the pole from the zeta term at $s=0$ and the poles of the gamma function at negative even integers to the left of zero.

Note that in a neighborhood of zero, we have $$\frac{1}{x^s} = 1 - \log(x) s + \frac{1}{2} \log^2(x) s^2 + \sum_{q\ge 3} \frac{(-1)^q}{q!} \log^q(x) s^q$$ and $$\zeta(s+1) = \frac{1}{s} + \gamma - \gamma_1 s + \sum_{q\ge 2} \frac{(-1)^q}{q!} \gamma_q s^q$$ and $$\Gamma(s) = \frac{1}{s} - \gamma + \left(\frac{\gamma^2}{2}+\frac{\pi^2}{12}\right) s + \cdots$$ and finally $$\cos(\pi s/2) = 1 - \frac{\pi^2}{8} s^2 + \frac{\pi^4}{384} s^4 + \sum_{q\ge 3} (-1)^q \frac{\pi^{2q}}{2^{2q}\times (2q)!} s^{2q}.$$

Collecting the contributions to $1/s$ we get $$-\log(x)s \times \frac{1}{s} \times \frac{1}{s} \times 1 + 1\times \frac{1}{s} \times -\gamma + 1\times \gamma \times \frac{1}{s}$$ and hence $$\mathrm{Res}\left(Q(s)/x^s; s=0\right) = -\log x.$$

Fortunately the residues from the remaining poles are simple to compute and summing all contributions we get $$\sum_{q\ge 1} \mathrm{Res}\left(Q(s)/x^s; s=-2q\right) = \sum_{q\ge 1} \frac{1}{(2q)!} (-1)^q \times x^{2q} \times -\frac{B_{2q}}{2q}.$$ This sum is in fact $$-\sum_{q\ge 1} \frac{(ix)^q}{q!} \frac{B_q}{q} + ix \times -\frac{1}{2}.$$ Recall that $$\sum_{q\ge 1} B_q \frac{t^q}{q!} = -1 + \frac{t}{e^t-1}$$ so that $$\sum_{q\ge 1} B_q \frac{t^{q-1}}{q!} = -\frac{1}{t} + \frac{1}{e^t-1}$$ and hence $$\sum_{q\ge 1} B_q \frac{t^q}{q\times q!} = -\log(t) + \log(e^t-1)- t.$$

This is $\sim -1/2 \times t$ in a neighborhood of zero so we can be sure no spurious constant has appeared during the integration.

We return to our collection of residues and finally obtain (setting $t=ix$) $$\log(ix) - \log(e^{ix}-1)+ ix - \frac{1}{2} ix -\log x = -\log(e^{ix}-1) + \log i + \frac{1}{2} ix \\= -\log e^{ix/2} -\log(e^{ix/2}-e^{-ix/2}) + \log i + \frac{1}{2} ix \\= -\log(2i\sin(x/2)) + \log i = -\log(2\sin(x/2)).$$

This holds for $x$ in $(0,2\pi).$ Observing that $S(x)$ is periodic with period $2\pi$ and even we get the end result $$-\log|2\sin(x/2)|.$$

Answer 5

We can ask Mathematica to sum the series and see what comes out.

Simplify[ComplexExpand[Re@Sum[Cos[n*x]/n, {n, 1, Infinity}]]]

$$-\log(2-2\cos(x))/2$$

Note that I've grabbed just the real part because numerical experiments show that the imaginary part is zero. Of course, we should always check these kinds of computations. Note for example, that this function has a logarithmic singularity at $x=0$, exactly as we'd expect, since the series boils down to the Harmonic series at $x=0$. We can also try to use the computer to compute the Fourier coefficients of the result. I can't quite seem to get the result fully symbolically, but here's a partial result:

(2/Pi) Table[
  Integrate[- Log[2 - 2 Cos[x]]*Cos[n*x]/2, {x, 0, Pi}],
{n, 1, 10}]
(* Out: {1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10} *)

Well, that looks good! I guess we could also look at a plot:

Plot[{
   -Log[2 - 2 Cos[x]]/2,
   Sum[Cos[n*x]/n, {n, 1, 15}]
 }, {x, -8, 8}]

Answer 6

The result can also be obtained by a much simpler derivation than given above.

Put $C(x) = \sum \frac{\cos(nx)}{n}$ then we first see that $C(\pi) = -(1-1/2+1/3-...) = -\log(2)$ and

$C(x) = C(\pi) + \int_\pi^x \frac{dC(x)}{dx}dx \\ = -\log(2) -\mathcal{Im}\left(\int_\pi^x\sum e^{inx}dx\right)\\ = -\log(2) -\int_\pi^x\frac{\sin(x)}{2-2\cos(x)}dx \\ = - \frac{\log|2-2\cos(x)|}{2}$

Answer 7

Here is a solution by doing complex integration in the upper half plane.

Define \begin{equation} f_n(\gamma) = \int_{\gamma = C(t)} \mathrm{e}^{\mathrm{i} n z} dz \end{equation} where $\gamma$ is a continuous path not defined yet but fixed. Each $f_n$ is analytic in the upper half plane and we require $\gamma \subset C^+(z)$, where if $z \in \gamma$, $\Re(z) > 0$.

Due to the uniform continuity of the integral in the upper half plane we assert that \begin{equation} f(\gamma) := \sum_{n=1}^{\infty} f_n = \int_{\gamma} \sum \mathrm{e}^{\mathrm{i} n z} d z \end{equation} but, using the geometrical series \begin{equation} \sum_{n=1}^{\infty} \mathrm{e}^{\mathrm{i} n z} = \frac{\mathrm{e}^{i z}}{1 - \mathrm{e}^{i z}} \end{equation} and so \begin{equation}a \sum_{n=1}^{\infty} f_n(\gamma) = \int_{\gamma} \frac{ \mathrm{e^{\mathrm{i} z}}}{1 - \mathrm{e^{\mathrm{i}z}}} dz \end{equation}a Call this equation (1). With the antiderivative: \begin{equation} \int \frac{\mathrm{e}^{\mathrm{i} z}}{1 - \mathrm{e}^{\mathrm{i} z}} = \mathrm{i} \log(1 - \mathrm{e}^{\mathrm{i} z} ) + \mathrm{constant} \end{equation}

We now worry about $\gamma$. Let $\gamma$ the straight segment $x + \mathrm{i} \epsilon$ that joins the points $x + \mathrm{i}\epsilon$ to $\pi/2 + \mathrm{i} \epsilon$, with $\epsilon > 0$, where $0< x \le \pi/2$ are real numbers, then \begin{eqnarray} f_n(\gamma) &=& \left .\frac{\mathrm{e}^{\mathrm{i} n z}}{\mathrm{i} \; n} \right |_{z=x + \mathrm{i}\epsilon }^{\pi/2 + \mathrm{i} \epsilon} \\ &=& \mathrm{e}^{-\epsilon n} \frac{ \mathrm{e}^{\mathrm{i} n \pi/2} - \mathrm{e}^{\mathrm{i}n x}} {\mathrm{i} \, n} \\ &=& \mathrm{e}^{-n \epsilon} \frac{\cos (n \pi/2) + \mathrm{i} \sin (n \pi/2) - \cos n x + \mathrm{i} \sin nx}{\mathrm{i} \; n} \\ \end{eqnarray} Then take the imaginary part of $f_n(\gamma)$ and get \begin{equation} \mathrm{Im}[ f_n(\gamma)] = \mathrm{e}^{-n \epsilon} \frac{ \cos nx + \cos n \pi/2 }{n} \end{equation} On the other hand \begin{eqnarray} \int_{\gamma} \frac{\mathrm{e}^{\mathrm{i} z}}{1 - \mathrm{e}^{\mathrm{i} z}} &=& \left . \mathrm{i} \log(1 - \mathrm{e}^{\mathrm{i} z} ) \right |_{z=x+\mathrm{i} \epsilon}^{\pi/2 + \mathrm{i} \epsilon} \\ &=& \mathrm{i}[ \log ( 1 - \mathrm{e}^{-\epsilon}\mathrm{e}^{\mathrm{i} \pi/2}) - \log(1 - \mathrm{e}^{-\epsilon} \mathrm{e}^{\mathrm i x})] \end{eqnarray} We now express this into its real and imaginary parts, but we are only interested on the imaginary part since that is what matches the series of cosines above. This is, we first find the modulus \begin{equation} \left | \frac{ 1 - \mathrm{e}^{-\epsilon \mathrm{i}} \mathrm{e}^{\mathrm{i} \pi/2}}{1 - \mathrm{e}^{-\epsilon} \mathrm{e}^{\mathrm{i} x}} \right | = \frac{\sqrt{ 1 + \mathrm{e}^{-2 \epsilon}}}{\sqrt{ \mathrm{e^{-2 \epsilon} \sin^2 x + (1 - \mathrm{e}^{-\epsilon} \cos x )^2 }}} \end{equation}

From which \begin{equation} \mathrm{Im} \int_{\gamma} \frac{\mathrm{e}^{\mathrm{i} z}}{1 - \mathrm{e}^{\mathrm{i} z}} = \log \frac{\sqrt{ 1 + \mathrm{e}^{-2 \epsilon}}}{\sqrt{ \mathrm{e^{-2 \epsilon} \sin^2 x + (1 - \mathrm{e}^{-\epsilon} \cos x )^2 }}} \end{equation}

So from equation(1) and the results shown where we match the imaginary components

\begin{equation} \sum_{i=1}^{\infty} \mathrm{e}^{-n \epsilon} \frac{ \cos nx + \cos n \pi/2 }{n} = \log \frac{\sqrt{ 1 + \mathrm{e}^{-2 \epsilon}}}{\sqrt{ \mathrm{e^{-2 \epsilon} \sin^2 x + (1 - \mathrm{e}^{-\epsilon} \cos x )^2 }}} \end{equation} Since the sum in the left converges uniformly for any $\epsilon > 0$, we can take the limit as $\epsilon \to 0$, inside the sum. \begin{equation} \sum_{i=1}^{\infty} \frac{ \cos nx }{n} + \sum_{i=1}^{\infty} \frac{ \cos n \pi/2 }{n} = - \frac{\log (1- \cos x)}{2} \quad , \quad 0 < x \le \frac{\pi}{2}. \end{equation} Now, \begin{equation} \sum_{i=1}^{\infty} \frac{ \cos n \pi/2 }{n} = \sum_{k=1}^{\infty} \frac{(-1)^k}{k} = - \log 2 \end{equation} Hence \begin{equation} \sum_{i=1}^{\infty} \frac{ \cos nx }{n} = - \frac{\log (2- 2 \cos x)}{2} \quad , \quad 0 < x \le \frac{\pi}{2}. \end{equation}

At this point we converted this in an exercise of analytic continuation. The function \begin{equation} f(z) = - \frac{\log (2- 2 \cos z)}{2} \end{equation} is analytic in the complex plane except for singularities at $z= 2 k \pi$, where $k$ is any integer.