5

I am trying to prove the above as an exercise in the topic of connectivity. I have tried to do so using ear decompositions, as odd degree vertices may be characterized as end points of ears, but to no avail. Any recommendations are appreciated. Thanks

ChristianHollis
  • 53

1 Answers1

11

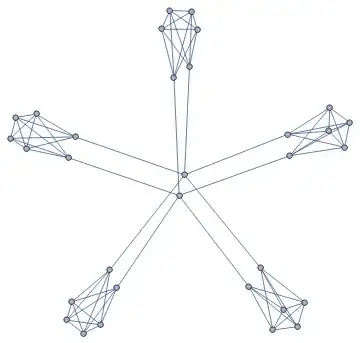
The statement is false. Take the following $5$-regular graph (inspired by the graph in this MathOverflow answer, which being $4$-regular didn't quite do the trick):

enter image description here

In this graph, every degree is odd, so we are looking for a Hamiltonian path. However, to visit each of the five parts around the sides, we would have to go through the middle vertices multiple times, so this is impossible.

For a slightly more formal argument: if a graph $G$ has a Hamiltonian path, it has a path $P_n$ as a subgraph. Deleting two vertices from $P_n$ leaves at most $3$ components, so the same must be true of $G$ (which is $P_n$ with extra edges). But in the graph above, deleting the two middle vertices leaves $5$ components, so it can't have a Hamiltonian path.

Misha Lavrov
  • 159,700
  • Maybe I’m missing something, but it looks like every vertex has degree four, and the question as it appears now is about paths that go through every odd-degree vertex. There are no such vertices in your graph. The Thomassen graphs here might be the example needed: http://mathworld.wolfram.com/ThomassenGraphs.html (oops, not, I think now...) – Steve Kass May 06 '19 at 00:23
  • 1
    Whoops - the MathOverflow question was about all $k$-regular graphs for $k=3$, so naturally this graph uses $k=4$ rather than $k=5$... I will fix this. – Misha Lavrov May 06 '19 at 00:27
  • 1
    (+1) Because the claim doesn't assume regularity, you can get a smaller (and planar!) counterexample by taking five $K_4$s rather than five $K_6$s. – hmakholm left over Monica May 06 '19 at 01:06
  • @HenningMakholm We could even take only four $K_4$s rather than five; then we wouldn't need to visit both cut vertices, but that's not the obstacle to begin with... – Misha Lavrov May 06 '19 at 01:10