4

We're given the following dynamical system:

$$ \begin{aligned} \dot x &= -x + y + x (x^2 + y^2)\\ \dot y &= -y -2x + y (x^2 + y^2) \end{aligned} $$

What's the largest constant $r_0$ such that the circle $x^2 + y^2 < r_0^2$ lies in the origin's basin of attraction?

So far, with relatively easy algebra, I've got:

$$ \begin{aligned} \dot r &= \frac{r}{2}(-2-\sin(2 \phi)+2r^2) \\ \dot \phi &= -(1+\cos^2(\phi)) \end{aligned} $$

Which immediately shows $r_0 \geq \sqrt{\frac12}$. How to show that there is no better bound?

Rodrigo de Azevedo
  • 23,223
Radost Waszkiewicz
  • 1,857
  • 8
  • 23
  • @LutzL You're correct. Edited the question to fix those bugs. – Radost Waszkiewicz May 04 '19 at 14:35
  • @AVK No need. It seemed like a good approach to me... If you mean directly integrate the equations to get explicit solution then that's a little disappointing method :( – Radost Waszkiewicz May 04 '19 at 17:19
  • I am sorry, I was mistaken :( – AVK May 04 '19 at 18:44
  • 1
    Numerical simulation indicates that $r_0$ is not equal to $1/\sqrt2$, but approximately 0.84. $x^2+y^2<1/\sqrt2$ is the largest positive invariant level set, but not the largest level set that lies in the origins basin of attraction – AVK May 04 '19 at 18:51
  • @AVK, too bad this is not something that can be easily calculated. If you could make this an answer (with a graphic maybe) we could close this question. – Radost Waszkiewicz May 05 '19 at 10:45
  • If we take $(x, y) = A_\alpha (a r \cos \phi, b r \sin \phi)$ with $$a = \sqrt {1 + \frac 1 {\sqrt {13}}}, \quad b = \sqrt {1 - \frac 1 {\sqrt {13}}}, \quad \alpha = \arctan \frac {3 + \sqrt {13}} 2,$$ where $A_\alpha$ is the counterclockwise rotation matrix, we'll get $$\dot r = - r (1 - r^2) \left( 1 + \frac {\cos 2 \phi} {\sqrt {13}} \right).$$ $a$ and $b$ are the axes of the elliptical basin of attraction, and $\alpha$ is the angle between its major axis and the $x$-direction. – Maxim May 08 '19 at 21:31
  • @Maxim This is correct but we're still left out with the nontrivial angular dependence. Where were you going with this? On top of that even if we get $\dot r < 0$ it's unclear if this relates in a simple way to the original circle. – Radost Waszkiewicz May 08 '19 at 21:33
  • @Maxim Oh, I see now. You're saying the elliptic basin can be derived analytically. (+1) Getting to the final radius from there is a matter of simple-ish algebra. This transformation is answer worthy at least! – Radost Waszkiewicz May 08 '19 at 21:45

3 Answers3

2

(This is only a "numerical" answer to the question)

A basin of attraction can be found numerically using reverse-time (or backward) integration. If we choose some initial point and integrate backwards for a sufficient time, we can obtain the set of the system states that it had before it reached the selected initial point. So, if we choose sufficiently many initial points that are contained in the basin of attraction (i.e. sufficiently close to the attracting steady state) and integrate backwards, we can get some idea of how the basin of attraction looks like.

The following picture demonstrates the aprroximation of the basin of attraction of the system: 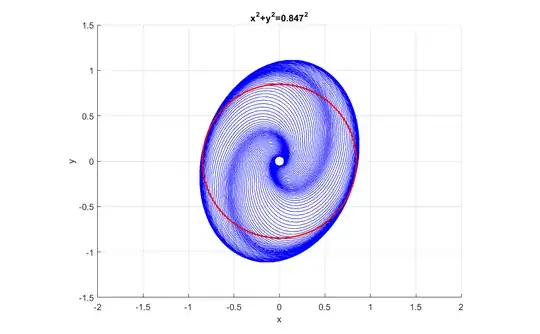enter image description here The blue curves fill the basin of attraction. The red circle is the largest circle that fits in the basin of attraction. I have choosen 36 initial points on the circle of radius 0.05. Here is the Matlab code:

axes 
hold on
r= 0.05; % radius of the circle of initial points
rpm= @(t,x)[-x(1)+x(2)+x(1)*(x(1)^2+x(2)^2);...
-x(2)-2*x(1)+x(2)*(x(1)^2+x(2)^2)]; % the right part of the system
for fi= 0:pi/36:2*pi
        % notice the backward in time direction of integration
    [t,z]= ode45(rpm,15:-0.1:0,r*[cos(fi) sin(fi)]);
    plot(z(:,1),z(:,2),'b');
end
grid on
h= ezplot('x^2+y^2=0.847^2',[-2 2],[-1.5 1.5]); % draw the circle
h.LineWidth= 1.7;
h.Color= 'red';
axis equal
AVK
  • 5,333
  • 1
    You can compute the limit cycle as boundary value problem with the period as parameter. Evaluating points on this solution gives $0.8500906724312877$ as minimal distance to the origin. – Lutz Lehmann May 07 '19 at 18:17
1

After solving the system

$$ \dot r = \frac{r}{2}(-2-\sin(2 \phi)+2r^2) \\ \dot \phi = -(1+\cos^2(\phi)) $$

we have

$$ \left\{ \begin{array}{rcl} r & = & \frac{\sqrt{3} \sqrt{3-\cos \left(2 \sqrt{2} \left(t-2 c_1\right)\right)}}{\sqrt{3 e^{2 t} c_2-\cos \left(2 \sqrt{2} \left(t-2 c_1\right)\right)+\sqrt{2} \sin \left(2 \sqrt{2} \left(t-2 c_1\right)\right)+9}} \\ \phi & = & -\tan ^{-1}\left(\sqrt{2} \tan \left(\sqrt{2} t-2 \sqrt{2} c_1\right)\right) \\ \end{array} \right. $$

Regarding the $r$ behavior the line of maxima after considering $c_1 = c_2 = 0$ is given by

$$ r_{max} = \frac{\sqrt{3} \sqrt{3-\cos \left(2 \sqrt{2} t\right)}}{\sqrt{\sqrt{2} \sin \left(2 \sqrt{2} t\right)-\cos \left(2 \sqrt{2} t\right)+9}} $$

with $\min r_{max} = \sqrt{1-\frac{1}{\sqrt{13}}}\approx 0.850088$

Cesareo
  • 36,341
0

Since the limit cycle looks like an ellipse centered at the origin, we'll try to find a Lyapunov function $V = a x^2 + b x y + c y^2$ s.t. $\dot V = (A x^2 + B x y + C y^2 + D) (V - V_0)$. This only requires equating the coefficients of two polynomials in $x$ and $y$, yielding, up to a constant factor, $$V = 8 x^2 - 2 x y + 5 y^2, \\ \dot V = 2 (x^2 + y^2) (V - 6).$$ $V = 6$ is the equation of the limit cycle; the radius of the maximal circle is the minor semiaxis of the ellipse.

Maxim
  • 11,274