1

I know that in arbitrary division rings, one can go about finding inverses Euclidean division. But take $\mathbb Z_{11}$ as a simple example. Is there a "nice" expression which yields the inverses in general? i.e. an expression $e(n)$ such that

$$ e(1) = 1, \quad e(2) = 6, \quad e(3) = 4, \quad e(4) = 3, \quad e(5) = 9, \quad e(6) = 2, \quad e(7) = 8, \quad e(8) = 7, \quad e(9) = 5, \quad e(10) = 10, $$

all up to mod 11.

I tried polynomial interpolation, but ended up with this ugly thing:

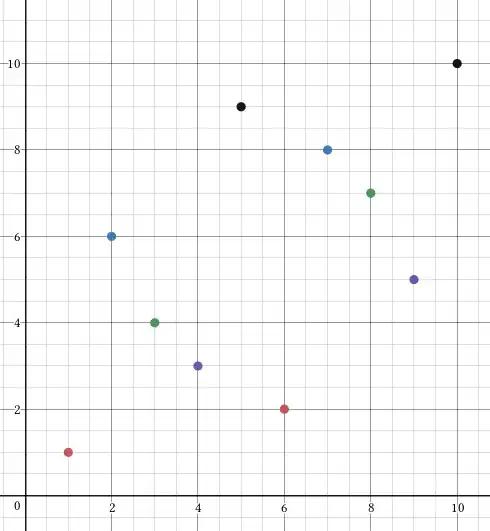
$$-\frac{7 x^9}{2160}+\frac{77 x^8}{480}-\frac{4279 x^7}{1260}+\frac{28919 x^6}{720}-\frac{4653 x^5}{16}+\frac{1911679 x^4}{1440}-\frac{4091593 x^3}{1080}+\frac{2321143 x^2}{360}-\frac{1229503 x}{210}+2123,$$

which isn't surprising, given the points it should pass through:

enter image description here

Naturally this does not account for modulo 11, so probably one can get something better if polynomial interpolation can be adapted up to mod 11. Or maybe the expression isn't a polynomial at all, maybe it can include a factorial term? I'm mentioning this because I tried to play around with Wilson's theorem but this didn't yield anything immediately useful.

Luke Collins
  • 8,838
  • To find inverses, you need the extended Euclidean algorithm in general. Only in special cases, they can be found easier. – Peter Apr 22 '19 at 12:57
  • For small $a$ we can give an explicit formula (closed form) for $,a^{-1}\bmod n,$ using Inverse Reciprocity, e.g. I do that here for $,a = 5.,$ But generally this involves about $\ a/2,$ cases so it is not practical for large $,a.$ $\ \ $ – Bill Dubuque Apr 22 '19 at 14:20

1 Answers1

3

Yes, there is a nice and simple polynomial (over the field $\mathbb F_p$): namely, $$ x \mapsto x^{p-2}. $$ If you want to map the integers $[0,p-1]$ to themselves, combine this with the fractional part function: $$ x\mapsto p\left\{\frac{x^{p-2}}{p}\right\}. $$

W-t-P
  • 4,709
  • 1
    Yes that is indeed a simple formula ! More generally, the inverse of $a$ mod $m$ when $\gcd(a,m)=1$ is $a^{\phi(m)-1}$. But, for large $p$, it is slower than the Euclidean Algorithm as a means of calculating $a^{-1}$. – Derek Holt Apr 22 '19 at 13:07
  • Of course, because $\mathbb F_p\setminus {0}$ is a group! I can't believe I missed this. Thank you. – Luke Collins Apr 22 '19 at 13:07
  • 1
    @DerekHolt, if we use square-and-multiply as an algorithm for computing the power mod $p$, it only takes $O(\log p)$ steps, I think. – paul garrett Apr 22 '19 at 13:35
  • 1
    @paulgarrett That's true, but according to the discussion here it is still slower than using the extended euclidean algorithm. – Derek Holt Apr 22 '19 at 14:00