1

Let $x$ have a uniform density

$f_x(x\mid\theta) \sim U(0,\theta)=\left\{ \begin{array}{ll} \frac{1}{\theta} & 0 \leq x \leq \theta \\ 0 & \text{otherwise} \end{array} \right.$

If there are $n$ samples $D=\{x_1,x_2,...,x_n\}$ drawn independently according to $f_x(x\mid\theta)$; then:

How can I show that the maximum likelihood of $\theta$ is $\max[D]$?

Ali J.
  • 101
  • It's rather trivial, just write down the likelihood function. You should find that it is a decreasing function of $\theta$ except for a jump discontinuity at $\theta=\max[D]$. – Ian Apr 21 '19 at 14:02
  • See https://math.stackexchange.com/q/2941187/321264, https://math.stackexchange.com/q/649678/321264. – StubbornAtom Apr 21 '19 at 14:05
  • Maybe a 'duplicate, but that doesn't mean there are no more insights to be gained from additional discussion. – BruceET Apr 22 '19 at 03:41

1 Answers1

0

The MLE is the maximum $W$ of the sample $X_i, X_2, \dots, X_n,$ as illustrated in the figure below. This MLE cannot be found by differentiation because the likelihood function is discontinuous at its maximum.

The true parameter value is $\theta = 7.$ The likelihood function for a particular sample of size $n=10$ is shown in the interval $(2, 15).$ The largest value in the sample is $W = 6.926851.$

You should formulate a mathematical argument that describes what you see in the figure.

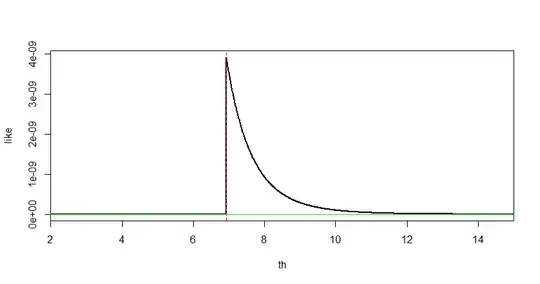
enter image description here

th = seq(2,15, by=.01); n=10;  m=length(th)
like = numeric(m)

x = runif(n, 0, 7); sort(round(x, 4))   
[1] 0.4111 2.6044 3.2130 4.1652 4.5213
[6] 4.7329 6.0148 6.0578 6.6110 6.9269
w = max(x);  w
[1] 6.926851

for(i in 1:m) {
  like[i] = prod(dunif(x, 0, th[i])) }
plot(th, like, type="l", lwd=2, xaxs="i")
  abline(v=w, col="red", lty="dashed")
  abline(h=0, col="green2")

Note: Obviously, the MLE is biased. The maximum $W$ of the data can never exceed $\theta.$ But $E\left(\frac{n+1}{n}W\right) = \theta.$

BruceET
  • 52,418