OEIS sequence A280984 (based on this Math Stack Exchange question) describes the
minimum number of dominoes on an $n \times n$ chessboard to prevent placement of another domino.
The sequence begins:
0, 2, 3, 6, 9, 12, 17, 22, 27, 34, 41, 48, 57, 66, 75
Fifteen terms are known, and a few folks have conjectured that $$ A280984(n) = \left\lceil \frac {n^2}3 \right\rceil \text{ for } n > 1. $$
Andrey Zabolotskiy has a proof that (1) this is a lower bound, and (2) this conjecture holds when $n$ is a multiple of $3$.
In order to prove the conjecture it is sufficient to give a tiling strategy for the $(3n+1)\times(3n + 1)$ and $(3n+2)\times(3n+2)$ boards.
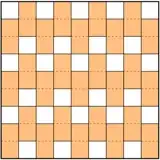
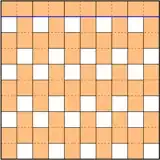
Example of $3n \times 3n$ boards.
To achieve this bound for the $3n \times 3n$ boards you can just do the naive placement, but for the other boards, it's not clear which placement strategy to use.
(Notice that the second and third examples are not optimal: the last two boards have $35$ tiles and $42$ tiles respectively, but there exist $34$ and $41$ tile placements.)
Question
Is there simple strategy for the $(3n+1) \times (3n+1)$ and/or the $(3n+2) \times (3n+2)$ boards that attains the lower bound? Or is the conjecture false?