Integral involving complex exponential function

Question

I am trying to solve the following integral:$$\int_0^∞\frac{e^{-α(u+iπ/2)}\exp(te^{u+iπ/2})}{(u+iπ/2)^{β+1}}\,\mathrm du-\int_0^∞\frac{e^{-α(u-iπ/2)}\exp(te^{u-iπ/2})}{(u-iπ/2)^{β+1}}\,\mathrm du$$with $α,t>0$ and $\Re β>-1$.

I am not able to simplify. It seems that may be solve using complex analysis with Cauchy Theorem and a appropriate path.

Note that second integral is the conjugate of first one.

Any help will be welcome.

Answer 1

HINT

$\color{brown}{\textbf{Contour integrals.}}$

Given integral can be presented in the form of $$I = \int\limits_{C_{\Large_\rightarrow}} f(w)dw + \int\limits_{C_{\Large_\leftarrow}} f(w)dw,\tag1$$ where $$f(w)=e^{-\alpha w} w^{-(\beta+1)} e^{\large te^{\Large w}},\tag2$$ contour $C_{\Large_\rightarrow}$ is line $$w=u+i\frac\pi2,\quad\text{where}\quad u = 0 \to\infty.$$ contour $C_{\Large_\leftarrow}$ is line $$w=u-i\frac\pi2,\quad\text{where}\quad u = \infty \to 0.$$ Let $$C_{\Large_\uparrow}: w=0+iv,\quad\text{where}\quad v=-\frac\pi2\to \frac\pi2,$$ $$C_{\Large_\rightarrow}(R): z=u+i\frac\pi2,\quad\text{where} \quad u = 0 \to \ln R,$$ $$C_{\Large_\downarrow}(R): z=\ln R+iv,\quad\text{where} \quad v=\frac\pi2\to -\frac\pi2,$$ $$C_{\Large_\leftarrow}(R): z=u+i\frac\pi2,\quad\text{where} \quad u = \ln R\to0.$$ then $$C_{\Large_\rightarrow} = \lim\limits_{R\to\infty}C_{\Large_\rightarrow}(R),\quad C_{\Large_\leftarrow} = \lim\limits_{R\to\infty}C_{\Large_\leftarrow}(R),\tag3$$ $$I = \lim\limits_{R\to\infty} I_R,\quad\text{where} \quad I_R=\int\limits_{C_{\Large_\rightarrow}(R)} f(w)dw + \int\limits_{C_{\Large_\leftarrow}(R)} f(w)dw,\tag4$$

At the same time, the contour $$C = C_{\Large_\uparrow} + C_{\Large_\rightarrow}(R)+C_{\Large_\downarrow}(R) + C_{\Large_\leftarrow}(R)$$ is closed, and there are not special points inside.

Therefore, $$\int\limits_{C_{\Large_\uparrow}} f(w)dw + \int\limits_{C_{\Large_\rightarrow}(R)} f(w)dw + \int\limits_{C_{\Large_\downarrow}(R)} f(w)dw + \int\limits_{C_{\Large_\leftarrow}(R)} f(w)dw = 0,$$ $$I_R = \int\limits_{C_{\Large_\rightarrow}(R)} f(w)dw + \int\limits_{C_{\Large \leftarrow}(R)} f(w)dw = -\int\limits_{C_{\Large_\downarrow}(R)} f(w)dw - \int\limits_{C_{\Large \uparrow}} f(w)dw.\tag5$$

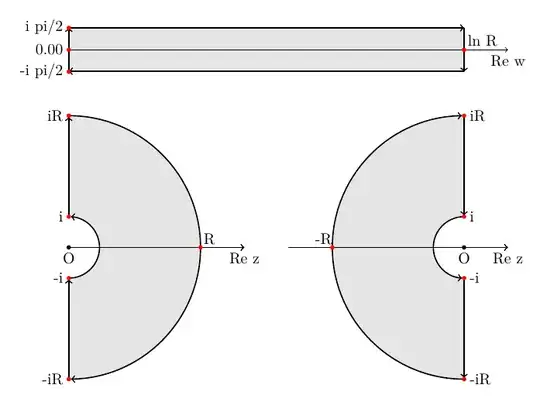
Substitution $$z=e^w,\quad dw = \dfrac{dz}z$$ provides the equalities $$I_R = -\int\limits_{D_{\Large_\curvearrowright}(R)}g(z)\,dz - \int\limits_{D_{\Large_\curvearrowleft}(R)}g(z)\,dz = \int\limits_{D_{\Large_{\uparrow-}}(R)}g(z)\,dz + \int\limits_{D_{\Large_{\uparrow+}}}g(z)\,dz = -\int\limits_{E_{\Large_\curvearrowright}(R)}g(z)\,dz - \int\limits_{E_{\Large_\curvearrowleft}}g(z)\,dz, \tag6$$ where $$g(z) = z^{-(\alpha+1)}(\ln z)^{-(\beta+1)}e^{tz}\,dz,\tag7$$ $$D_{\Large_{\uparrow+}}: z=0+iy,\quad\text{where}\quad y=1\to R,$$ $$D_{\Large_\curvearrowright}(R): z=Re^{i\varphi},\quad\text{where} \quad \varphi = \dfrac\pi2 \to \dfrac{3\pi}2,$$ $$D_{\Large_{\uparrow-}}(R): z=ye^{\Large \frac{3\pi}2i},\quad\text{where} \quad y=R\to 1,$$ $$D_{\Large_\curvearrowleft}(R): z=e^{i\varphi},\quad\text{where} \quad \varphi = \dfrac{3\pi}2\to\dfrac\pi2.$$ $$E_{\Large_\curvearrowleft}: z=e^{i\varphi},\quad\text{where} \quad \varphi = \dfrac\pi2\to -\dfrac\pi2.$$ $$E_{\Large_{\uparrow-}}(R): z=ye^{\Large -\frac{\pi}2i},\quad\text{where} \quad y=R\to 1,$$ $$E_{\Large_\curvearrowright}(R): z=Re^{i\varphi},\quad\text{where} \quad \varphi = -\dfrac{\pi}2 \to \dfrac\pi2,$$

Easy to show that $$\lim\limits_{R\to\infty} \int\limits_{E_{\Large_\curvearrowright}}g(z)\,dz = 0.$$

Therefore, $$I = -\int\limits_{E_{\Large_\curvearrowleft}}g(z)\,dz + \int\limits_{E_{\Large_{\uparrow-}}(\infty)}g(z)\,dz - \int\limits_{D_{\Large_{\uparrow-}}(\infty)}g(z)\,dz,$$ $$ = i\int\limits_{\Large\frac\pi2}^{\Large\frac{3\pi}2}\,e^{-i\alpha\varphi}(i\varphi)^{-(\beta+1)}e^{\large te^{\Large i\varphi}}\, d\varphi +\int\limits_1^\infty \left(\left(\ln y+i{\small\frac32}\pi\right)^{-(\beta+1)} - \left(\ln y-i\frac\pi2\right)^{-(\beta+1)}\right) y^{-\alpha}e^{-ity}\,dy.$$