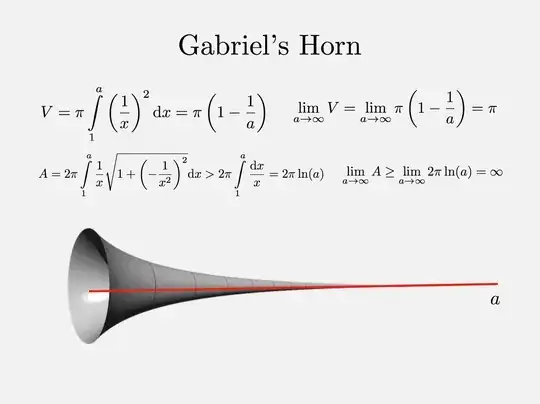
What is the principle at play? Differing degrees?
Asked
Active
Viewed 534 times
2 Answers
4
If you have a gallon of paint that you can roll out as thin as you please, then you can paint any wall, no matter how large.
B. Goddard
- 33,728
-
The great 20th century mathematician John von Neumann once said to a student, "Young man,in mathematics one does not understand things. One merely gets used to them." – DanielWainfleet Feb 28 '19 at 17:38
-
-
2
In 3-D there is no positive lower limit to the ratio of volume to area for a bounded surface. E.g. for an arbitrarily narrow piece of a hose. So if you can patch together a sequence of bounded surfaces with volume-to-area ratios $V_n/A_n\to 0$ (as $n\to \infty$) such that $\sum_nV_n<\infty =\sum_nA_n$ then you have a result as in Gabriel's Horn.
Let $x$ be the L-to-R co-ordinate along the direction of the red axis. For $n\in \Bbb Z^+ $ the area $A_n$ of the part of Gabriel's Horn between $x=n$ and $x=n+1$ is more than the area of the curved wall of a cylinder of length $1$ and radius $1/(n+1),$ which is $\frac {2\pi}{n+1},$ while the volume $V_n$ of that same part of Gabriel's Horn is less than the volume of a cylinder of length $1$ and radius $1/n,$ which is $\frac {2\pi}{n^2}.$ So for the total area $A$ and volume $V$ we have $$V<\sum_{n=1}^{\infty} \frac {2\pi}{n^2}<\infty =\sum_{n=1}^{\infty}\frac {2\pi}{n+1}\le A .$$
DanielWainfleet
- 59,529
-
Some fast-food chains serve salt obtained from a 100+ year-old process that grows narrow conical salt crystals from brine. So a greater proportion of a sprinkle of their salt will directly contact your taste buds than will occur with common cubical salt crystals. They haven't yet achieved $ V/A=0.$ – DanielWainfleet Feb 28 '19 at 18:31