find the maximum and minimum of $\sum_{i=1}^{n} (10x^3_{i}-9x^5_{i})$

Question

Let $x_{i}\ge 0$ such that $$x_{1}+x_{2}+\cdots+x_{n}=1.$$ Find the maximum and minimum of $$f=10\sum_{i=1}^{n}x^3_{i}-9\sum_{i=1}^{n}x^5_{i}.$$

I have proved $n=2$ $$1\le f\le\dfrac{9}{4}$$ see: wolfarma

When $n=3$, How prove that $10(a^3+b^3+c^3)-9(a^5+b^5+c^5)\le\dfrac{9}{4}$

So I suspect that the general positive integer $n\ge 4$, also has the following conclusion $$1\le f\le \dfrac{9}{4}$$ when $$(x_{1},x_{2},\cdots,x_{n})=(1,0,0,\cdots,0),f=1$$ and $$(x_{1},x_{2},\cdots,x_{n})=(0,\dfrac{1}{2}+\dfrac{1}{2\sqrt{3}},\dfrac{1}{2}-\dfrac{1}{2\sqrt{3}},0,\cdots,0),f=\dfrac{9}{4}$$But how to prove or reverse this conclusion?

Answer 1

Assumption

If $f(x)$ is convex strictly increasing for $0 \le x \le 1$ then

$$ \min\sum_{k=1}^n f(x_k) \ \ \mbox{s. t. }\ \ \sum_{k=1}^n x_k = 1, \ \ x_k > 0 $$

has it's minimum at $ x_1 = \cdots = x_n = \frac 1n$

Using Lagrange Multipliers the problem can be stated as

$$ L(x,\lambda) = \sum_{k=1}^n f(x_k)-\lambda\left(\sum_{k=1}^n x_k -1\right) $$ so the stationary points are the solutions for

$$ \frac{d}{dx_k}f(x_k) -\lambda = 0\\ \sum_{k=1}^n x_k - 1 = 0 $$

or

$$ x_k = \frac{\sqrt{5\pm\sqrt{5} \sqrt{5-\lambda }}}{\sqrt{15}} $$

now assuming all $x_k = \frac{\sqrt{5+\sqrt{5} \sqrt{5-\lambda }}}{\sqrt{15}}$

so

$$ \lambda = \frac{15(2n^2-3)}{n^4} $$

then

$$ x_k =\left\{\frac 1n,\frac{\sqrt{\sqrt{\frac{\left(n^2-3\right)^2}{n^4}}+1}}{\sqrt{3}}\right\} $$

The last value is discarded because does not observe the restriction then we follow with $x_k = \frac 1n$ so

$$ \min \sum_{k=1}^n f(x_k) = n f\left(\frac 1n\right) $$

Attached a plot showing the $F_n(x_n^*) = \sum_{k=1}^n f(x_n^*)$ evolution assuming $n$ continuous

NOTE

$$ f(x) = 10x^3-9 x^5 $$

is convex strictly increasing for $0\le x \le 0.5 $ so for $n \gt 2$ we have at $x^* = \frac 1n$ a local minimum.

For $n = 2$ making $x_2=\lambda x_1, \ x_3 = \mu x_1$ we have

$$ \min_{\lambda,\mu}\frac{10(1+\lambda^3+\mu^3)}{(1+\lambda+\mu)^3}-\frac{9(1+\lambda^5+\mu^5)}{(1+\lambda+\mu)^5} $$

which gives the feasible solution

$$ x_1 = x_2 = \frac 12 $$

Answer 2

For $n\geq4$ the minimal value is not $1$.

For example, take $n=4$ and $x_1=x_2=x_3=x_4=\frac{1}{4}.$

We'll prove that for $n\geq3$ the minimal value it's $\frac{10n^2-9}{n^4}$ and occurs for $x_1=x_2=...=x_n=\frac{1}{n}.$

Indeed, we need to prove that $$\sum_{k=1}^ng(x_k)\geq ng\left(\frac{\sum\limits_{k=1}^n}{n}\right),$$ where $g(x)=10x^3-9x^5,$ which has unique inflection point $x_0=\frac{1}{\sqrt3}$ on $[0,1]$.

Thus, by Vasc's HCF Theorem it's enough to prove our inequality for

$x_1=x_2=...=x_{n-1}=a$ and $x_n=1-(n-1)a,$ which gives $$(na-1)^2(9n^3(n^3-4n^2+6n-4)a^3-9n^2(3n^3-7n^2+3n+3)a^2+n(17n^3+2n^2-18n-18)a+n^3+n^2-9n-9)\geq0,$$ which is true because $$9n^3(n^3-4n^2+6n-4)a^3-9n^2(3n^3-7n^2+3n+3)a^2+$$ $$+n(17n^3+2n^2-18n-18)a+n^3+n^2-9n-9\geq0$$ for all $n\geq3$ and $0\leq a\leq\frac{1}{n-1}.$

The proof of the last statement for you.

The hint for the maximal value.

Since $g$ has an unique inflection point on $[0,1]$,

we can use Karamata and Jensen and we can get an inequality of one variable.

For $n=4$ it works very well, but for $n\geq5$ it's very ugly.

Answer 3

Since $$x_n=1-\sum_{i=1}^{n-1} x_i,\tag1$$ then required to find the least and the greatest values of $$F_n(\vec x) = \sum_{i=1}^{n-1} (10x_i^3-9x_i^5)+10x_n^3-9x_n^5\tag2,$$ where $$\vec x = \{x_1,x_2\dots x_{n-1}\},\quad x_k\ge0,\quad k=1,2\dots n.\tag3$$

The problem of bounds is not actual, because the arbitrary quantity of points can be set to zeros.

$\color{brown}{\textbf{The stationary points.}}$

The stationary points of $F$ can be defined from the system $$\frac{\partial F_n}{x_k}=0,\quad\text{where}\quad k=1,2\dots n-1,$$ or \begin{align} &30(x_k^2-x_n^2)-45(x_k^4-x_n^4) = 0,\quad k=1,2,\dots n-1,\\[4pt] &(x_k-x_n)(x_k+x_n)(2-3x_k^2-3x_n^2) = 0,\quad k=1,2,\dots n-1.\\[4pt] \end{align} If $x_n$ is known, then, taking in account the constraints $(3),$ vector $\vec x$ WLOG can be presented in the form of $$ \vec x = \left\{\underbrace{\sqrt{\frac23-x_n^2}\dots\sqrt{\frac23-x_n^2}}_{n-m},\underbrace{x_n\dots x_n}_{m-1}\right\},\\[8pt] m=1\dots n.\tag4 $$ I.e. exactly $m$ unknowns set to $x_n,$ and the other $(n-m)$ set to $\sqrt{\frac23-x_n^2}\,.$

$\color{brown}{\textbf{Case }\quad\mathbf{m=n.}}$

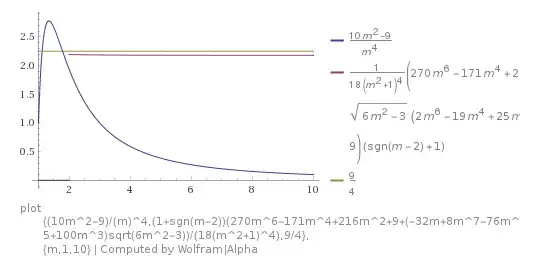
Solution for the inner stationary points is $$\begin{align} &\vec x = \left\{\underbrace{\frac1n\dots\frac1n}_{n-1}\right\},\quad x_{n}=\frac1n,\\ &F_n\left(\vec x\right) = \frac{10}{n^2}-\frac9{n^4},\\[4pt] &\dfrac{\partial}{\partial n}F_n\left(\vec x\right) = \frac{4(9-5n^2)}{n^5},\\[4pt] &\min_n F_n\left(\vec x\right) = \lim_{n\to\infty} F_n\left(\vec x\right) = 0,\\[4pt] &\max_n F_n\left(\vec x\right) = \frac{31}{16}\quad\text{at}\quad n=2,\quad x_n=\frac12 \end{align}$$ (see also Wolfram Alpha plot).

Taking in account the bounds of area, vector $\vec x$ can consist an arbitrary number of zeros instead of $x_n$.

So for the given $n$

$$F_n\left(\vec x\right)\in\left[\frac{10-9n^2}{n^4},\frac{31}{16}\right].\tag5$$

Note that if $n>3$ then $\min F\left(\vec x\right) < 1$ in the inner stationary points.

In paricular, if $n=4$ then $\min F\left(\vec x\right)= \dfrac{151}{256}.$

$\color{brown}{\textbf{Case }\quad\mathbf{m<n.}}$

Let $$s=n-m,\quad s\ge 1,\tag6$$ then \begin{align} &sx_1+mx_{s+m} = 1, \quad\text{where}\quad x_1=\sqrt{\frac23-x_{s+m}^2},\\[4pt] &P(x_{s+m},m) = 0, \quad\text{where}\quad P(x) = 3(mx-1)^2 + s^2(3x^2-2), \quad mx_{s+m}\le 1,\\[4pt] &3(m^2+s^2)x_{s+m}^2 - 6mx_{s+m} + 3 - 2s^2 =0,\\[4pt] &x_{s+m} = \dfrac{3m \pm s\sqrt{6(m^2+s^2)-9\phantom{\big|}}}{3(m^2+s^2)} = \dfrac{9m^2-6s^2(m^2+s^2)+9s^2}{3(m^2+s^2)(3m \mp s \sqrt{6(m^2+s^2)-9\phantom{\big|}}},\\[4pt] &x_1 = \dfrac{3m^2+3s^2-3m^2 \mp ms\sqrt{6(m^2+s^2)-9\phantom{\big|}}}{3s(m^2+s^2)} =\dfrac{3s \mp m\sqrt{6(m^2+s^2)-9\phantom{\big|}}}{3(m^2+s^2)}, \end{align} and, using the symmetry of $(x_{s+m},x_1)$ by $(s,m),$ $$\begin{align} x_{s+m} = \dfrac{3m \pm s\sqrt{6(m^2+s^2)-9\phantom{\big|}}}{3(m^2+s^2)} = \dfrac{3-2s^2}{3m \mp s\sqrt{6(m^2+s^2)-9\phantom{\big|}}},\\ \quad x_1=\dfrac{3s \mp m\sqrt{6(m^2+s^2)-9\phantom{\big|}}}{3(m^2+s^2)} = \dfrac{3-2m^2}{3s \pm m\sqrt{6(m^2+s^2)-9\phantom{\big|}}}. \end{align}\tag7$$

Note.

• $P(0) = 3-2s^2,\quad P\left(\frac1m\right)=s^2,$ so $P(0)\not=0,\quad P\left(\frac1m\right)\not= 1.$

Easy to see that the numerator of $x_{s+m}$ in $(7)$ is negative iff $s=1,$ i.e. $m=n-1.$

Let us consider the case $s=1$ apparently.

$\textbf{Case }\mathbf{n=2,\quad m=1,\quad \dbinom sm = \dbinom11.}$

From $(7)$ should $$x_2 = \dfrac{3 - \sqrt3}6 = \dfrac1{3 + \sqrt3},\quad x_1 = \frac{3 +\sqrt3}6 =\dfrac1{3-\sqrt3},$$ $$F_2\left(\overrightarrow{\{x_1\}}\right) = 20\dfrac{3^3+3\cdot3^2}{6^3} - 18\dfrac{3^5+10\cdot3^4+5\cdot3^3}{6^5} = \dfrac94.$$

$\textbf{Case }\mathbf{n \ge 3,\quad m=n-1,\quad \dbinom sm \in \dbinom1{[2, \infty)}.}$

From $(7)$ should $$\begin{align} &x_{n} = \dfrac{3m - \sqrt{6m^2-3\phantom{\big|}}}{3(m^2+1)} = \dfrac1{3m + \sqrt{6m^2-3\phantom{\big|}}},\\ &x_1=\dfrac{3 + m\sqrt{6m^2-3\phantom{\big|}}}{3(m^2+1)} = \dfrac{3-2m^2}{3 - m\sqrt{6m^2-3\phantom{\big|}}},\\ &\vec x = \left\{x_1,\underbrace{x_n\dots x_n}_{m-1}\right\},\\ &F_n\left(\vec x\right) =\dfrac{30m^6-19m^4+24m^2+1}{(m^2+1)^4} +\dfrac{8m^7-76m^5+100m^3-32m}{9(m^2+1)^4}\sqrt{6m^2-3\phantom{\big|}},\\ \end{align}$$ (see also Wolfram Alpha plot),

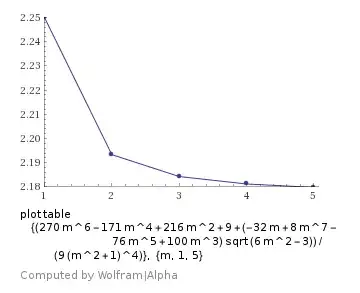
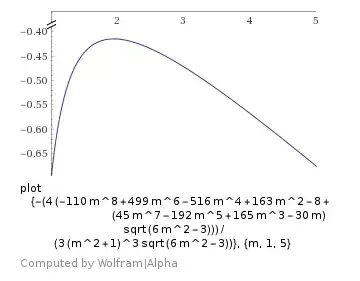
wherein the derivative $$\dfrac\partial{\partial n} F\left(\vec x\right) = \dfrac{4(110m^8-499m^6+516m^4-163m^2+8 + \sqrt{6m^2-3\phantom{\big|}}(-45m^7+192m^5-165m^3+30m)}{3(m^2+1)^5\sqrt{6m^2-3\phantom{\big|}}}$$ less than zero $\forall (m\ge2)$ (see also Wolfram Alpha factor plot)

$\textbf{Case }\mathbf{n \ge 4,\quad m=n-s,\quad \dbinom sm \in \dbinom{[2, \infty)}{[n-s, \infty)}.}$

Taking in account $(7)$ and $(4),$ can be written \begin{align} &\vec x = \left\{\underbrace{x_1\dots x_1}_{n-m},\underbrace{x_n\dots x_1}_{m-1}\right\},\\ &x_n = \dfrac{3m + s\sqrt{6(m^2+s^2)-9\phantom{\big|}}}{3(m^2+s^2)} = \dfrac{2s^2-3}{s\sqrt{6(m^2+s^2)-9\phantom{\big|}}-3m},\\[4pt] & x_1=\dfrac{3s - m\sqrt{6(m^2+s^2)-9\phantom{\big|}}}{3(m^2+s^2)} = \dfrac{3-2m^2}{3s + m\sqrt{6(m^2+s^2)-9\phantom{\big|}}},\\[4pt] &\left[\begin{aligned} &\begin{cases} m=0\\ x_1=\dfrac1s \end{cases}\\[4pt] &\begin{cases} m=1\\ x_n = \dfrac{3 + s\sqrt{6s^2-3\phantom{\big|}}}{3(s^2+1)} = \dfrac{2s^2-3}{s\sqrt{6s^2-3\phantom{\big|}}-3}\\ x_1=\dfrac{3s - \sqrt{6s^2-3\phantom{\big|}}}{3(s^2+1)} = \dfrac1{3s + \sqrt{6s^2-3\phantom{\big|}}} \end{cases}\\[4pt] \end{aligned}\right. \end{align} Easy to see that this case leads to the previous solutions.

$\color{brown}{\textbf{Conclusion.}}$

Therefore, $$F_n\left(\vec x\right)\in\left\{\dfrac{10}{n^2}-\dfrac9{n^4},\dfrac94\right\}$$ (see also Wolfram Alpha plot).