Will a path between $(x, y)$ and $(-x, -y)$ always intersect a 90 degree rotated copy?

Question

Suppose we have a path between two points $(x, y)$ and $(-x, -y)$. If we rotate it by 90 degrees around the origin, will the copy intersect the original? (You can add any number of assumptions to avoid pathological cases.)

It seems obvious that it does (if you play with a construction you can see how changing the curve in one place to avoid an intersection with the copy makes it intersect in another place) but I cannot come up with a way to show it. My guess is there is a simple observation I am missing.

Background: This is a technical step in a demonstration that polyominoes that cover two opposite corners of their hull can only tile a rectangle in a certain way. This step comes in to show that if you rotate a polyomino 90 degrees and it does not overlap the original, it also does not overlap the original when you rotate it 180 degrees.)

Edit: After getting a feel for it from the posted answers, I realize it's much more technical than I thought and probably not appropriate for what I wanted to use it for.

Edit: Actually, this answer given to a version of this question works well for my purposes. Also, see this more general question.

Answer 1

This proof assumes there is no "backtracking" or radial movement (i.e. every line through the origin intersects the curve in exactly one point, with the obvious exception of the line through $(x, y)$ and $(-x, -y)$, which intersects the curve twice). Also, the curve is continuous and goes counterclockwise around the origin from $(x, y)$ to $(-x, -y)$.

Take the line through the origin and $(-y, x)$ ($90^\circ$ counterclockwise rotated copy of $(x, y)$). If the curve intersects the line at $(-y, x)$ we are done. If not, it intersects the line either outside or inside $(-y, x)$. Let's say inside (like your yellow, green and orange examples). Then the $90^\circ$ rotated curve goes on the inside of $(-x, -y)$.

This means that if we take a continuous "sweep" of lines through the origin, starting with the one through $(-y, x)$ and ending with the one through $(-x, -y)$, then the original curve goes from being on the inside of the rotated curve to being on the outside. By the intermediate value theorem they must intersect.

Answer 2

Edit $\quad$ This answer misses the situations where a curve does not fall under the two cases mentioned (see the following image for two examples). It is also possible that $Y$ from the first case is empty (for instance, when $D=C$). However, this does not affect the outcome. One last point; I realize that the third assumption is not so easily justified (take as an example a curve that intersects itself infinitely many times). We, therefore, need a specific definition of a curve that does not allow infinite self-intersections to avoid complications.

---

Here is an idea:

We can make the following assumptions:

A.1 $\quad$ As YiFan says, we can assume without loss of generality that the points are $A=(-1,0)$, $B=(1,0)$, $A'=(0,-1)$, and $B'=(0,1)$.

A.2 $\quad$ The curve $C$ connecting $A$ to $B$ does not pass through $A'$ or $B'$. (The statement is trivially true in such cases.)

A.3 $\quad$ The curve $C$ does not intersect itself. (Given such a curve, we can simply take another curve that is a subset of it with no self-intersections.)

We then have two cases:

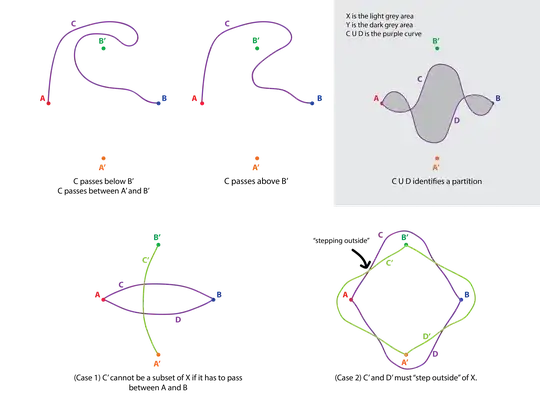
Case 1 $\quad$ The curve $C$ passes "below" $B'$ and "above" $A'$. Let $D$ be $C$ rotated about the origin $180$ degrees. Clearly $C\cup D$ identifies a partition of the plane; The "perimeter" $P$ of $C\cup D$, the unbounded subset $X$ consisting of points "outside of" $P$, and the bounded subset $Y$ (possibly empty; see above) consisting of points "inside of" $P$. If the curve $C'$ is a subset of $X$, then it will not be "going between" $A$ and $B$ as it is supposed to, therefore it has a point shared with $P$, and we are done.

Case 2 $\quad$ The curve $C$ passes "above" $B'$ or "below" $A'$. We consider only the former, and the latter is similar. Again, we let $D$ be the rotation of $C$ by $180$ degrees, and we have $P$, $X$, and $Y$ as in case 1. In this case we know that $A'$ and $B'$ are in $Y$. If the curve $C'$ along with its $180$ degree rotation $D'$ want to identify, using their perimeter, a bounded subset of the plane that contains $A$ and $B$ (as they are supposed to), then they must "step outside" of $X$. And when they do so, they intersect $P$, and we are done again.

Below are five figures that help illustrate the idea:

---

The above can be formalized using concepts of elementary topology, and the not-so-elementary theorem known as Jordan Curve Theorem. I will try to post a formal answer once I know what to do with the cases I am missing.

For now, I will give a few formulations that can motivate a formalization.

By Jordan Curve Theorem, every closed curve ($C \cup D$ in our application) divides the plane into at least two path-connected components, one of which is the unbounded exterior which I call $X$. The union of the other bounded components is what I call $Y$, and the perimeter $P$ is the closure of $Y$ without $Y$'s interior.

As to what I mean by "below" or "above": Given a curve $C$, we walk on it from $A$ to $B$, and we take note how we travel by writing a sting $\rho$ of Greek letters. If we pass through the region of the $Y$-axis below $A'$, we write $\alpha$ for going left-to-right and $\alpha^{-1}$ for going right-to-left. Similarly, we use $\beta$ and $\gamma$ for the region between $A'$ and $B'$ and the region above $B'$, respectively. We use $\delta$ (or $\epsilon$, respectively) when we make a clockwise rotation around $A$ (or $B$), and $\delta^{-1}$ (or $\epsilon^{-1}$) for a counterclockwise turn. Then we verify that Case 1 deals with those curves whose reduced $\rho = \sigma \beta \tau$, where $\sigma$ (or $\tau$, respectively) only refers to rotations about $A$ (or $B$). While Case 2 deals with those where $\rho = \sigma \alpha \tau$ or $\sigma \delta \tau$, where $\sigma$ and $\tau$ are as before. Furthermore, the situations which I miss are those whose $\rho$ does not have such a form.

Answer 3

(Note I missed a case which makes the proof invalid; I leave my answer for now in case it can be saved. The missing case is 3.3.)

---

The core idea of Arthur's proof is to go from "inside" to "outside" smoothly, we need an intersection. Putting this together in a slightly different way, we can arrive at what I wanted to show without too many assumptions.

(Edit 2: Turns out this lemma is, in fact, false: https://math.stackexchange.com/a/3123629/67933)

Lemma. Suppose we have a closed curve that passes through $A = (x, y)$ and $B = (-x, -y)$. This curve intersects a rotated (by any amount, around the origin) copy of itself.

Proof. Let $A'$ be the point on the copy that corresponds to $A$, and $B'$ the point that corresponds to $B'$. If either $A'$ or $B'$ lie on the original curve, we are done, so let's suppose they don't.

1. If one of $A', B'$ lies inside the original and the other outside, then the curves must intersect (as we move from the one along the copy, we must go from outside to inside at some point - a point of intersection).

2. If both $A', B'$ lie inside the original curve, then if no other point of the copy lie inside the original, the entire copy lies inside the original, which is impossible (they curves must surround the same area, but the inner one must have a smaller area than the outer one). [This step probably needs some work to account correctly for self-intersecting curves, cases where the area is 0, and other pathologies. For my original purposes it is enough to exclude these cases. Another possibility is to restrict rotations to integer fractions of a full rotation.] Therefor, some point of the copy must lie inside, and as before this implies the paths must intersect.

3. If both $A', B'$ lie outside the original curve, then either:

   1. The curves intersect and we are done;
   2. The copy lies completely inside the original, which is impossible as before; or
   3. The curves do not intersect and one is not inside the other. [Edit 1: I just discovered there is a problem in this case.]

Theorem. Suppose we have a path $P$ between two points $(x,y)$ and $(−x,−y)$. It intersects a copy rotated 90 degrees around the origin.

Proof. Rotate $P$ 180 degrees round the origin to form a new path $Q$ and 270 degrees to form a new path $Q'$.

Now we have a closed curves $PQ$ that passes through $(x, y)$ and $(−x,−y)$, and a copy $P'Q'$, rotated 90 degrees around the origin. These two curves must intersect each other by the lemma.

WLG assume this intersection point lies on $P$ in the original curve. It must then either lie on $P'$ or $Q'$. If it lies on $P'$, we are done. If it lies on $Q'$, the result follows from symmetry (just make all clockwise rotations anti-clockwise.)

Answer 4

I think there is a very simple proof. (The idea came from some of Marwan's pictures.)

Combine the curve with its 180 degree rotated copy. These form a region. This region MUST either contain or intersect (0,0). Do the same with the 90 degree and 270 degree copies. Thus, both regions contain or intersect (0,0). Since the two regions are the same size, one cannot contain the other without overlapping borders. Therefore, the boundaries must intersect (or overlap). From the symmetry, the original and 90 degree rotated version must intersect.