What is the difference between a unit simplex and a probability simplex?

Question

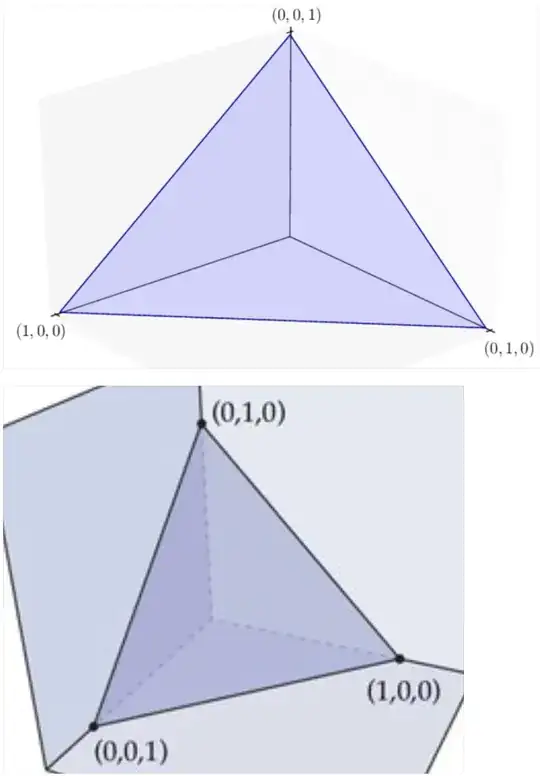
The unit simplex is the $n$-dimensional simplex determined by the zero vector and the unit vectors, i.e., $0,e_1, \ldots,e_n\in\mathbf R^n$. It can be expressed as the set of vectors that satisfy $$x\succcurlyeq0,\quad\mathbf 1^\mathrm T x\le1.$$ The probability simplex is the $(n−1)$-dimensional simplex determined by the unit vectors $e_1,\ldots ,e_n\in\mathbf R^n$. It is the set of vectors that satisfy $$x\succcurlyeq 0,\quad \mathbf 1^\mathrm T x=1.$$

I know that a simplex is the set of all convex combinations of some vectors. I can imagine that in two dimensions, the probability simplex is a right triangle with legs $\mathbf e_1$ and $\mathbf e_2$. In three dimensions, it is a right tetrahedron with legs $\mathbf e_1$, $\mathbf e_2$ and $\mathbf e_3$. But what does the unit simplex look like? What difference can the zero vector make?

Answer 1

From your definition, the probability simplex is the subset of the unit simplex in which the sum of the elements of the vector is exactly one, i.e., $\sum_{i=1}^n x_i = 1$.

In two dimensions, the unit simplex is the triangle formed by coordinates (0,0), (0,1) and (1,0), whereas the probability simplex is the line joining (1,0) and (0,1).

Note that the probability simplex has one dimension less than the unit simplex. This is precisely because the probability simplex is constrained by $\sum_{i=1}^n x_i = 1$, so you lose one degree of freedom. In the two dimensional case, when you choose a value for $x_1$, $x_2$ is immediately pinned down ($x_2 = 1 - x_1$) in the probability simplex. For the unit simplex, in contrast, $x_2 \leq 1 - x_1$ is not pinned down by $x_1$.

Answer 2

The vectors $\{x_i\}_{1\le i\le n+1}$ comprise a regular simplex. Because all vertices are contained within the hyperplane with the equation $$\sum_{1\le i\le n+1}a_i\ x_i=1$$ it clearly is just $n$D. Its dihedral angle measured across the margins equally is given by $$\arccos(1/n)$$ All edges of that regular simplex obviously have size $\sqrt 2$.

When adjoining to the origin, then you'll still have a simplex, then sure being $(n+1)$D. But the slope of the lacing facets here is not so steep as would for the regular one (of according dimension). In fact the lacing margins would clearly show up dihedral angles of $90°$ each. - The size of the base edges here still is $\sqrt 2$, while the size of the lacing edges, i.e. those connecting to the origin, clearly is just $1$.

--- rk

Answer 3

• The top figure is unit simplex (tetrahedron), which is the convex hull of 4 points: (0,0,0),(1,0,0),(0,1,0),(0,0,1).
• The bottom figure is probability simplex (triangle), which is the convex hull of 3 points: (1,0,0),(0,1,0),(0,0,1). It is one face of the tetrahedron.