Coloring grid points with two colors

Question

Let $S$ be a set of finite many grid points (points in the coordinate system with integer coordinates). Is it always possible to color them with two colors, red and blue, such that in each vertical and horizontal line the following statements is true:

if there are $R$ number of red and $B$ number of blue points, than $|R-B|\leq 1$?

This is an olympiad combinatorics problem (from 1986), but I still can’t solve it. I tried to find strategies to color them, but now I am not even sure that the statement is true.

Answer 1

Let $C$ be the condition on a line (row/column) that number of red points differs from the number of blue points by at most $1$.

We shall prove the statement by induction on the number of grid points $n=|S|$. Suppose all sets with number of grid points $<n$ can be coloured with red and blue points such that in each row and column, $C$ is satisfied. We shall now prove the statement for $n$ grid points.

Case 1: There is atleast one row or column with an odd number of elements

Call the said row/column $L$. In this case we pick any point $P$ from $L$ and apply our induction hypothesis on $S- \{P\}$, to obtain a colouring of $S- \{P\}$. The number of points in $L- \{P\}$ is even, and therefore must contain equal number of Red and Blue points if it is to satisfying condition $C$. Thus, whether we colour P blue or red, condition $C$ is still satisfied for $L$. Let $L_2$ be the line through $P$ perpendicular to $L$. We colour P red if the number of blue points in $L_2- \{P\}\geq$ number of red points in $L_2- \{P\}$ and blue otherwise. This colouring of $S$ satisfies $C$ for all rows and columns and we are done.

Case 2: All rows and columns have an even number of elements

This case is trickier.

Pick any point $P_1$ and draw a horizontal line through it extending towards either right or left (which ever side has at least $1$ point). Let $P_2$ be the first point it meets. $P_2$ must exist as all rows and columns have an even number of elements. Now draw a vertical line through $P_2$, extending towards either up or down (which ever side has at least $1$ point), and let $P_3$ be the first point it meets. Draw a horizontal line through $P_3$ and so on. Let $j$ be the least number such that $P_j=P_i$ for some $i<j$.($j=11$ in the figure) If $i$ and $j$ have the same parity(for $i=3$ in the figure), $P_iP_{i+1}$ and $P_{j-1}P_{i}$ are perpendicular. If not (if for example, $i=2$ in the figure), increment $i$ by 1. Then, for the new $i$, $P_iP_{i+1}$ and $P_{j-1}P_{i}$ are perpendicular.

Here is a diagram for illustration.

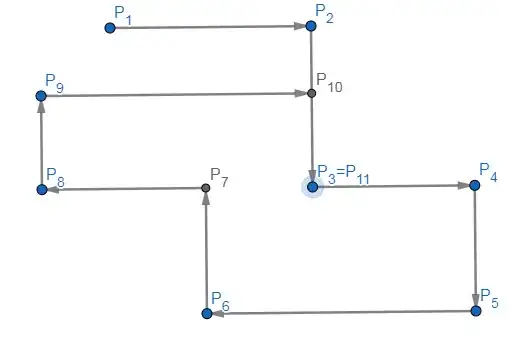
Let $S'=\{P_i,P_{i+1},...,P_{j-1}\}$. We apply induction hypothesis on $S-S'$ and colour $P_i$ blue, $P_{i+1}$ red, $P_{i+2}$ blue and so on till $P_{j-1}$ is coloured Red.

Any line in S goes through a number of pairs of adjacent points of S' with different colours, and through points of $S-S'$ and therefore satisfies $C$. Hence, we are done.

(The base case is trivial and left as an exercise.)

$\blacksquare$

Answer 2

Let $V=\{v_1,v_2,...v_n\}$ be a set of vertical and $H=\{h_1,h_2,...h_m\}$ set of horizontal lines which have vertices from the set $S$ and connect line $v_i$ with line $h_j$ iff $v_i\cap h_j \in S$, so we get a bipartite graph $G= (V,H)$.

• So the edges of this graph $G$ are vertices of $S$ (and vertices in $G$ are lines in $V$ and $H$).
• It is enough to prove the statement for connected components of $G$.

So let $K$ be any component in $G$ and we procede with induction on $|G|$.

Take any cycle $C$ in $K$ and color it edges alternatively red and blue. Since $G$ has only even cycles this means that each vertex in this cycle $C$ has one red and one blue edge. So if we "delete" all edges of $C$ in $K$ we get $K'$ and we can apply induction on $K'$ and we are done.

Now if there is no cycle in $K$ then $K$ is a tree so we have (at least) two leaves $l,l'$. Take path $P$ from $l$ to $l'$ and color edges again alternatively. Since $l$ and $l'$ have only one edge we are done for them and all other vertices on this path $P$ have again one red and one blue edge. So, if we "delete" all edges on this path we get new $K'$ and we can again use induction on $K'$ and we are done again.