8

This is a question regarding the definition of continuity.

My understanding of continuity is that a function is continuous at a point when it holds that $$\lim_{x\to a^-}f(x) = f(a) = \lim_{x\to a^+}f(x) \quad \quad (1)$$

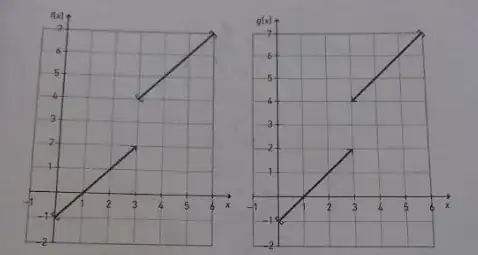
The book I'm currently reading has this image:

enter image description here

Note here that $f(x)$ is defined for $x=3$, but $g(x)$ is not.

This is followed by text stating that

g(x) is continuous because $D_g = [0, 6]\text{\\}\{3\}$, thus it is continuous for all values in its domain.

My point of contention here is that, how can we say that it is continuous at $x=3$ when $g(3)$ does not exist? Referring to the aforementioned definition $(1)$ that the limits converge to the actual value at this point.

I would have immediately declared both cases as jump discontinuities.

Am I mistaken here? Does $g(x)$ illustrate an exception to $(1)$?

Alec
  • 4,174
  • 8
    It is nowhere said that $g$ is continuous at $x=3$. – Martin R Nov 20 '18 at 10:01
  • 1
    There is a theorem saying that $g:D\to\cdots$ is continuous iff $g$ is continuous at every $x\in D$. Here $3\notin D$ so is irrelevant if it comes to the question whether $g$ is continuous. See here for a related question. – drhab Nov 20 '18 at 10:06
  • Also potentially relevant: If there are finitely many points where there are discontinuities, then $g$ is continuous almost everywhere. – Sam Benner Nov 20 '18 at 19:06

2 Answers2

19

$G$ is continuous on the domain $[0,3)\cup(3,6]$.

Referring to the aforementioned definition (1) that the limits converge to the actual value at this point.

3 is not in the domain. For every point in the domain of $g$, we have the required convergence.

user3482749
  • 6,750
  • It seems so obvious to me now. Why would I even consider the point at which the function is not defined? So why would that point have any impact on the continuity of the function? – Alec Nov 20 '18 at 14:37
  • 1
    @Alec, don't chastize yourself. I'd say many make this "visual" error; the example is maximally counter-intuitive to drive home its point after the reader has understood the issue (i.e., it is designed to destroy the naive intuition that "continuous" means that you can draw everything with a pen without lifting it..., which was literally the motivation for "continuous" at least in school (for pupils 15'ish years old, some decades ago) in my neck of the woods). – AnoE Nov 20 '18 at 16:39
  • @AnoE - Good point. I've been outspoken about how the (Norwegian) curriculum introduces limits in a single breath, only so that we can learn differentiation, which is a huge part of the curriculum. But we don't really learn limits. And so I don't see why students need to learn continuity until they've solidly grasped limits (with the epsilon/delta definition). I would have liked to see epsilon/delta earlier in the curriculum, or continuity later. So now we're learning limits the simplified way, and same with continuity (don't lift the pen). Inaccurate! Anyway, ventilation over. – Alec Nov 20 '18 at 16:54
3

The function is continuous everywhere in the interval except that point deleted from the domain, it's more a nuance of the language than anything else. Choose any point that is not $3$ in that interval: you can then find left- and right-hand limits to that point and show they're equal.

PrincessEev
  • 50,606