I am trying to prove the following conjecture:
Let it be $R_m(n) / m>0, m\in \Bbb N$ some reduced residue system modulo $n$ such that $R_m(n)$ is the reduced residue system between $(m-1)n$ and $mn$, and such that some element of the reduced residue system is a prime number.
Let it be $\lambda(R(n))$ the function expressing the number of consecutive reduced residue systems $R_m(n)$ (starting at $m=1$).
I conjecture that $\lambda(R(n))$ is always greater than $n$; that is, it exists some $R_m(n)$ for every $m \le n$.
In fact, I have checked that $\lambda(R(n))$ is much bigger than $n$, at least so it seems for $n \le 140$, as showed at this table I have calculated:
Values of $\lambda(R(n))$ for $n \le 140$
I would appreciate some advice and literature on the subject. Thanks in advance!
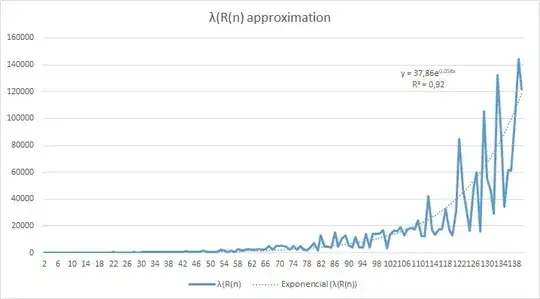
Edit: Below I have posted a graphic of $\lambda (R(n))$ with an approximation of the trend to an exponential function: