A question in SVD

Question

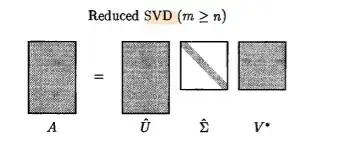
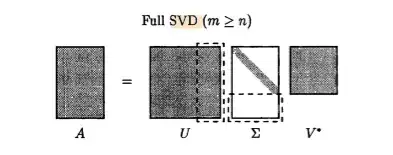
if $A\in \mathbb{R}^{m \times n}$, then SVD of A is $U\Sigma V^T$. I've seen different version of SVD. In the first one, $U\in \mathbb{R}^{m \times m}$, $\Sigma \in \mathbb{R}^{m\times n}$, and $V \in \mathbb{R}^{n\times n}$. In the second one $U\in \mathbb{R}^{m \times r}$, $\Sigma \in \mathbb{R}^{r\times r}$, and $V \in \mathbb{R}^{r\times n}$, where $r$ is the rank of $A$. Is there difference in these two forms or does one of them have an advantage over the other one? For instance when $U$ and $V$ are square matrices, then they are invertible, i.e, $U^TU=UU^T=I$. but when $U$ is not square only $U^TU=I$ is true.

Second question. if $A=U\Sigma V^T$, I've seen that $U^TU=I$. Can we deduce that $UU^T=I$, too?

score 1 · Answer 1 · 2018-10-15T02:21:09.900

1

First question

It follows from the definition of the SVD. The first one

$$ A_{m \times n} = U_{m \times m} \Sigma_{m \times n} V_{n \times n}^{T} \tag{1} $$

is the full SVD

the second one

$$ A_{m \times n} = U_{m \times r} \Sigma_{r \times r} V_{r \times n}^{T} \tag{2} $$

is the truncated SVD or reduced SVD where $A$ has rank $r$

visually we see the difference

Second question

It follows from the definition of the SVD. $U$ is orthogonal, which means that

$$ U^{T}U = UU^{T} = I \tag{3} $$

Note

In the SVD

$$ \sigma_{1} \geq \sigma_{2} \geq \cdots \sigma_{r} \geq 0 \tag{4} $$

if you multiply

$$ U_{m \times m} \cdot \Sigma_{m \times m} V_{m \times n}^{T}\tag{5} $$

and there are only $r$ singular values then it is $0$ after that. A diagonal matrix simply multiplies across. So we only care about

$$ U_{m \times r}\Sigma_{r \times r} V_{r \times n}^{T} \tag{6} $$

edited Oct 15 '18 at 02:21

answered Oct 14 '18 at 00:01

But if we write $U=[U_1 U_2]$, where $U_1 \in \mathbb{R}^{m\times r}$ and $U_2 \in \mathbb{R}^{m\times (m-r)}$, then $I_{m\times m}=UU^T=U_1U_1^T+U_2U_2^T$. Why $U_2U_2^T=0$? – S_Alex Oct 14 '18 at 00:33
https://math.stackexchange.com/questions/1771013/null-space-from-svd – Oct 14 '18 at 00:39
sorry that doesn't make sense...I think – Oct 14 '18 at 00:50
it equals zero because the singular values are zero past the rank $r$ – Oct 14 '18 at 01:01
you have $U_{n} \Sigma _{n} = 0 $ – Oct 14 '18 at 01:02
How is it related to $U_nU_n^T=0$? – S_Alex Oct 14 '18 at 01:05
I don't think your argument is true. As DiaryofNewton mentioned, $U_{m\times r}U_{m\times r}^T$ is not full rank, so it cannot be equal to $I_m$, as $I_m$ is full rank. – S_Alex Oct 14 '18 at 01:13
the rank of the matrix is $r$ – Oct 14 '18 at 01:13
the only matrix necessary is $U_{1}$ – Oct 14 '18 at 01:14
try making such a matrix... – Oct 14 '18 at 01:14
some demonstration $U$ has full rank $A$ is rank deficient – Oct 14 '18 at 01:28
Could you give argument rather than simulation? – S_Alex Oct 14 '18 at 01:28
turns out I was wrong, doesn't work – Oct 14 '18 at 01:42

DiaryofNewton · Answer 2 · 2018-10-14T00:38:31.490

0

Basically these two forms are equivalent. The second form can be deduced from the first form, whose elements are those of the second form and lots of zero, So when applied to data storage the second form take advantage, because you can ignore plenty of zeros and thus deal with a lower dimension. Another thing is, if U is not a square matrix then the conclusion is not true. Take (0 1) as an example. Also you may consider the rank of UU' and U'U, one of whom can't be full-rank. But there's indeed a conclusion that they share the same nonzero egienvalues, including their dimension!

edited Oct 14 '18 at 00:38

answered Oct 14 '18 at 00:32

DiaryofNewton

79

But Ryan claims that it is true. – S_Alex Oct 14 '18 at 00:49

A question in SVD

2 Answers2

First question

Second question

Note