I’m looking at the hyperbolic system ${{\mathbf{u}}_t} + {\mathbf{A}}({\mathbf{u}},x,t){{\mathbf{u}}_x} = {\mathbf{h}}({\mathbf{u}},x,t)$ $\quad$ (1)
where ${\mathbf{u}}(x,t) \in {\mathbb{R}^n},\;\;x \in \mathbb{R},\;\;t \in [0,\infty ),\;$ and ${\mathbf{A}}({\mathbf{u}},x,t)$ is a real n-by-n matrix, and with characteristics $\frac{{dx}}{{dt}} = {\lambda _i}({\mathbf{u}},x,t)$.
Why is the domain of dependence for the solution ${\mathbf{u}}(x,t)$ at a point $(x,t)$ given by the interval on the x-axis bounded by all the n characteristics passing through the point $(x,t)$?
I’m reading a compendium on this and it doesn’t explain it very well. In the compendium it is shown how the system can be rewritten as ${{\mathbf{l}}_i}^T({{\mathbf{u}}_t} + {\lambda _i}{{\mathbf{u}}_x}) = {{\mathbf{l}}_i}^T{\mathbf{h}}$ by assuming that ${\mathbf{A}}$ is diagonalizable. Here ${{\mathbf{l}}_i}$ is the i-th left eigenvector of ${\mathbf{A}}$ and ${\lambda _i}$ is the corresponding i-th real eigenvalue. This gives an expression for the projection of the directional derivative of ${\mathbf{u}}(x,t)$ (along the vector $(1,{\lambda _i})$) onto ${{\mathbf{l}}_i}$ , so the solution propagates along the characteristics of the system. In the compendium, it is written that since the solution propagates along n characteristics, the solution ${\mathbf{u}}(x,t)$ at a point $(x,t)$ is determined by the initial data on the interval on the x axis which is bounded by all the n characteristics going through the point $(x,t)$. There is no proof for why this is the case, only a very brief sketch involving a system of the form (1) with two equations.
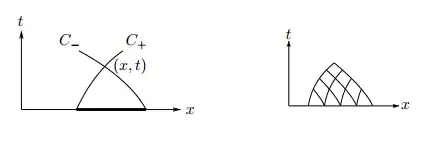
If $\frac{{dx}}{{dt}} = {\lambda _ - }$ and $\frac{{dx}}{{dt}} = {\lambda _ + }$ $\quad$ (2)
denote the two sets of characteristics ${C_ - }$ and ${C_ + }$ for a system of two equations, the author writes that one can then determine a discrete solution at a point $(x,t)$ by replacing the directional derivatives in (1) by difference formulas, and using known values of ${\mathbf{u}}$ on the two characteristics both passing through $(x,t)$. Then by making a grid of the characteristics (2), the solution can be determined from the initial data in the characteristic grid. See the figures below. If the grid is made finer, the discrete solution will converge to the continuous solution (there is no proof of this, as it’s outside the scope of the compendium to prove it).
I don’t understand this explanation. Is the domain of dependence every point in the interval or just a finite amount of points contained in the interval? Is there a simpler explanation for it (without going into the details of the proof of convergence of the discrete solution to the continuous solution), or any books where I can read about this?