7

First, I would like to introduce a peculiar way to display the prime numbers (greater than $9$) by means of the ten they belong to ($x$-axis), and their ending digit ($y$-axis).

Here's an example of such layout, reporting the first $25$ primes.

enter image description here

(You might be interested in the following conjecture, which is based on this two-dimensional representation of prime numbers).

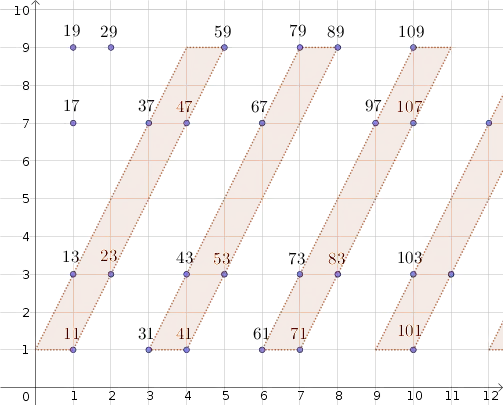
We can now organize the primes (except $17, 19,29$) in a series of parallelograms, defined by four points corresponding to the four integers $N+1$, $N+11$, $N+49$, and $N+59$, where $N=0,3,6, 9\ldots$ denotes an increasing number of tens ($N$-parallelogram).

enter image description here

As it was conjectured (and then shown) in this post, on the edge of each of these parallelograms, we can find at most $7$ primes.

The red crosses in the picture below indicate the "missing primes" for each $N$-parallelogram, i.e. the integers that lie on the $N$-parallelogram (in one of the eight positions in which we could locate a prime), but that are not prime numbers.

enter image description here

Now, we can easily see that the missing primes divisible by $7$ are located in a well defined position on each $N$-parallelogram, as one can easily verify in the following scheme:

enter image description here

Each gray segment, indeed, connects four missing primes divisible by $7$. For instance, the first segment from the left connects $49, 77, 133, 161$.

Similarly, we can recognize the missing primes divisible by $17$ in correspondence of the green segments in the following picture (again, four missing primes for each segment).

enter image description here

For instance, the first segment from the left connects the missing primes $119, 187, 323, 391$.

It is clear that this scheme can be generalized, always yielding to a neatly organized structure (somehow cylindrical) of missing primes.

Exactly here comes my question.

Given $N$, is there an elementary way to determine the exact number of missing primes, and their position, on the $N$-parallelogram?

I tried to use the interesting comments and the clever answers related to this post and also to this one, but I could not go far. Therefore, I will be very thankful for any suggestion.

I apologize in case of confusion and/or naivety, and I will ask you also to improve the correctness of this question.

Thanks again!

Community
  • 1
  • 1
    Remember, if you go very far to the right in your diagram, on average the prime numbers will become scarcer. For example, if you go far enough (something like $e^{1000}$), less than one out of every 1000 numbers will be prime (the Prime Number Theorem). Most of your parallelograms will hold no primes, only occasionally will there be one prime, two and more primes a really rare, etc. Even then, by usual conjectures (that have not yet been proved fully), you will have (very few!) parallelograms with many primes. Everybody expects that, but no proof has been found. – Jeppe Stig Nielsen Aug 21 '18 at 16:32
  • @JeppeStigNielsen Yes, true. Thanks for pointing this out. I am not an expert, and most likely my ideas are naive. I just thought that there could be a simple formula to guess the number of missing primes on the parallelograms, given the ordinate structures (constant slope, constant number of involved parallelograms, etc.) which I tried to depict in the last two plots. But, I see well your point. –  Aug 21 '18 at 16:37

1 Answers1

5

You are showing the Sieve of Eratosthenes in a new geometry. Your eight dots correspond to numbers not divisible by $2$ or $5$. Your lines connecting numbers divisble by $7$ are that stage of the sieve. The straight lines come because if you move over two tens and up one you get a new multiple of $7$ because $3 \cdot 7=21$l. You haven't dealt with multiples of $3$ that I can see. The lines for $17$ come because $3\cdot 17=51$ and so on.

Ross Millikan
  • 383,099
  • Thanks for your interesting answer, Ross! However, I am looking only for the numbers (and the position) of the integers lying on the parallelograms in the position in which we could find a prime (in other parallelograms), given $N$. Which is somehow less than to find all the primes. Do you think that the regularity of the lines can help to devise a strategy to solve this problem? Thanks again!! –  Aug 21 '18 at 05:19
  • Each successive prime will yield an new set of lines. They strike out all the multiples of that prime. It is just like striking out every $7th, 11th, 13th,$ etc number in the normal sieve. You achieve that sieving with the lines. As the primes get large the lines will be almost horizontal and you will need a lot of them. – Ross Millikan Aug 21 '18 at 05:24
  • I see! But there are anyway only $8$ positions to be assigned. Don't you think that there should be a sort of regularity in this assignment process, limited to these $8$ positions? –  Aug 21 '18 at 05:54
  • There is nothing magic about the parallelograms. If you just list the numbers in the arrangement you have done the fact that only the rows $1,3,7,9$ have dots reflects avoiding divisibility by $2$ and $5$, which divide $10$ so the divisibility test just uses the last digit. As I said, the straight lines you see are a consequence of modular arithmetic involving a prime and $10$. – Ross Millikan Aug 21 '18 at 15:48
  • Thanks again for your explanation, Ross. So, in conclusion you think that there is not a reasonable simple formula which gives the number (and/or the position) of missing primes in the $N$-parallelogram, do you? –  Aug 21 '18 at 15:57
  • No, that would be equivalent to a formula to produce the primes. The link between the parallelogram position and the number is simple. – Ross Millikan Aug 21 '18 at 16:00
  • I see! Thanks again, Ross! –  Aug 21 '18 at 16:01