How can I prove that at least 8 dominoes are required to allow a placement to which no further domino can be added without two dominoes sharing an edge
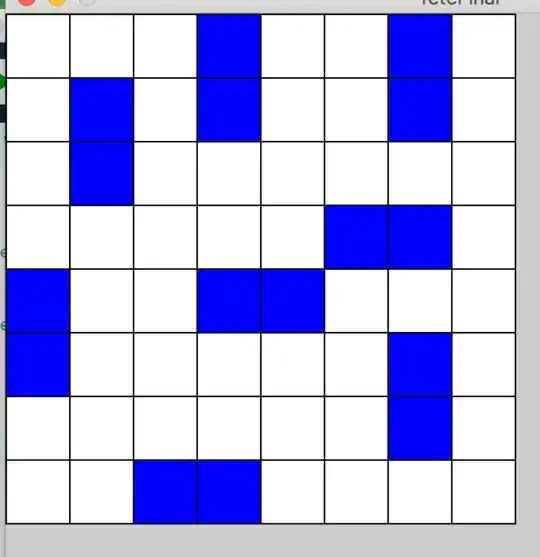
Any help will be appreciated.
How can I prove that at least 8 dominoes are required to allow a placement to which no further domino can be added without two dominoes sharing an edge

Any help will be appreciated.
For the ancient (2018), manual answer go further below.
The modern way to solve problems like this is through integer linear programming – which can always be further converted to a SAT instance, but such conversion is unnecessary here.
There are $112$ binary variables in this problem, the edges across which a domino may be placed. Each variable (edge) has a corresponding constraint expressing that "the virtual domino across this space shares an edge with at least one placed domino".
#!/usr/bin/env python3
from itertools import product
m, n = 8, 8
each edge is labelled by its upper or left square and its orientation (0 for H, 1 for V)
edges = [(i,j,0) for i in range(m-1) for j in range(n)] +
[(i,j,1) for i in range(m) for j in range(n-1)]
hitd = {}
for (n,(i,j,o)) in enumerate(edges):
same = [(i+dij[o],j+dij[1-o],o) for dij in product((-2,-1,0,1,2),(-1,0,1)) if abs(dij[0])+abs(dij[1]) < 3] # same orientation
same = [edges.index(e) for e in same if e in edges]
opp = [(i+dij[o],j+dij[1-o],1-o) for dij in product((-1,0,1,2),(-2,-1,0,1)) if abs(dij[0]-0.5)+abs(dij[1]+0.5) < 2.9] # opposite orientation
opp = [edges.index(e) for e in opp if e in edges]
for k in same + opp:
hitd[k] = hitd.get(k, []) + [n]
print("Minimize")
print("", " + ".join(f"x{n}" for n in range(len(edges))))
print("Subject To")
print("\n".join(" " + " + ".join(f"x{n}" for n in hh) + " >= 1" for hh in hitd.values()))
print("Binary")
print("", " ".join(f"x{n}" for n in range(len(edges))))
print("End")
The above Python program generates an LP file; run it through your favourite LP solver (I used HiGHS) and it will tell you that $8$ dominos is minimal, as claimed.
What seemed a simple question at first turned into a programming challenge. Yes, 8 dominos are required to mandate edge-to-edge contacts with further dominoes, but my eventual approach was somewhat strange…
Instead of thinking about the squares of the grid, think of the edges between adjacent squares, of which there are $2×8×7=112$. Now look at a domino:
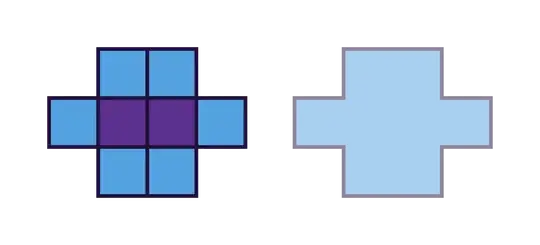
On the left, the domino itself is in a deep blue. A new domino makes edge-to-edge contact or overlaps the original domino iff the new domino overlaps a light blue square iff the edge between the new domino's two squares coincides with any of the short purple line segments. This set of at most 23 edges I will refer to as the original domino's zone (if close to the board's edge, some segments may lie off the board or fall on the board's boundary; we do not consider such edges).
The problem of placing dominos to mandate edge-to-edge contacts – a dominating covering – now becomes a problem of covering all 112 edges by domino zones. If an edge does not lie in any zone, it can serve as the middle edge of a new domino, with no edge contact.
Now consider the configurations of zones that can cover the two edges incident to a corner square. There are five distinct viable configurations up to reflection, which I will call type 1 to type 5 from left to right:
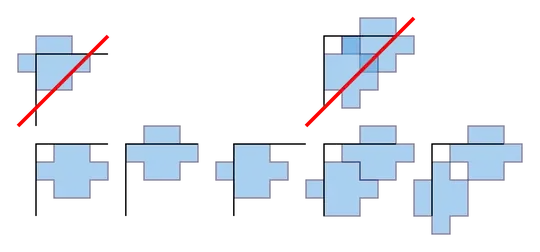
The two crossed-out configurations are not viable, because they can be replaced by the configurations immediately below them without uncovering any covered edges. Any dominating covering needs four of these configurations, one for each corner.
We can quite easily show that we can only use at most one instance of the type 4 and type 5 configurations combined. None of the configurations covers the following edges:
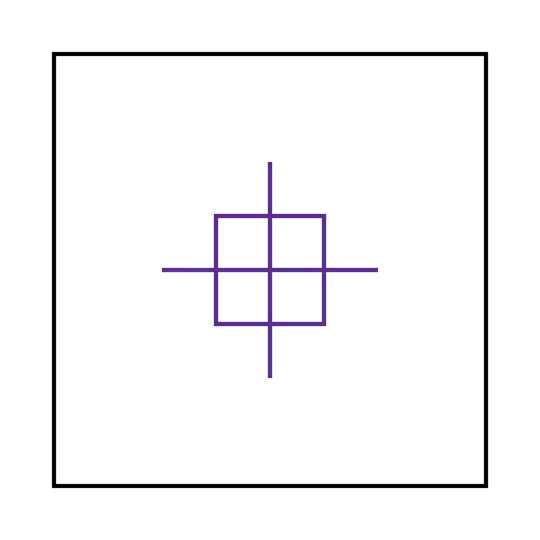
Furthermore, at least two zones are required to cover these edges, which means that the corner configurations can use at most five zones.
The last step is to prove that none of the combinations of corner configurations with five and four zones extend to a complete dominating covering on 7 dominos. For this I turned to the computer, brute-forcing each combination of corner configurations and remaining domino zones to show that every one of them could not cover all 112 edges, in a manner reminiscent of Zygalski sheets. The (Python + NumPy) code can be found here. Briefly, I eliminated type 5 from consideration first, showing that no dominating covering could use it. Then I did the same with types 4, 1, 2 and finally 3, proving the non-existence of 7-domino dominating coverings of the 8×8 board.
However, there do exist near-dominating coverings that cover 111 of 112 edges (leaving exactly one place for a new domino without making edge contact). Here is one:

The SVG source of the images in this answer can be found here.
Partial answer only...
Naming: We will call the initial set of dominoes the "blockers". They collectively make it impossible to place an "invader" domino without the invader sharing an edge with some blocker. The OP asks for a proof that $N=8$ blockers are necessary on an $8 \times 8$ board. My answer proves a lesser result:
If the blockers are not allowed to touch the board edges, then $N=8$ are necessary and sufficient.
Sufficiency:
8 . . . . . . . .
7 . x . x . x x .
6 . x . x . . . .
5 . . . . . x x .
4 . x x . . . . .
3 . . . . x . x .
2 . x x . x . x .
1 . . . . . . . .
a b c d e f g h
Necessity:
Since the blockers are not allowed to touch any board edge (in my version), some blocker must occupy b2 in order to prevent an invader at a12. Similarly blockers must occupy b7, g2 & g7. These 4 blockers, no matter how each is oriented, will leave de1, de8, a45, h45 as 4 possible locations for the invader. We will need an extra blocker to eliminate each of these 4 possible invader locations. Thus 8 blockers are necessary.
Further thoughts: As mentioned, this proof is incomplete. I tried to prove that allowing blockers to touch the board edges (as in the OP sample solution) cannot make the blocking task EASIER (i.e. $N < 8$), but without success... Simple transformations don't seem to work. E.g. in the OP solution, the blockers at a34 and cd1 collectively prevent any intruder at a1, and we cannot move either blocker off the board edge without a whole series of other moves.
Maybe this helps.
Least no. of dominoes which can be placed on $8\times 6$ rectangle is $4$. You can prove it by dividing $8\times 6$ rectangle into $4, 4\times 3$ rectangles.
The remaining $8\times 2$ grid can have 4 dominoes.
ceil(112/23)= 5(by using walls we can increase it to 6). So some other tricks should be used – Vasily Mitch Jul 19 '18 at 17:36