2

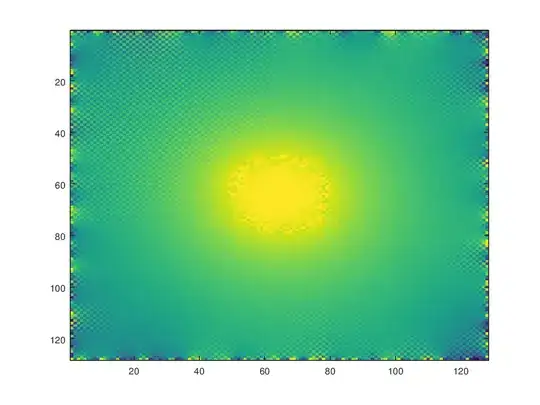
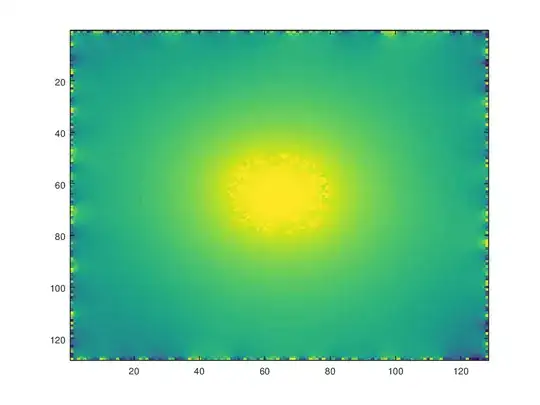
I am using finite difference software to solve across 1D line from x=0 to x=1 (left Domain), and x=1 to x=2 (middle/central domain) and x=2 to x=3 (right domain). The only difference between domains is that the central domain posses a source term.

I have a Left hand domain where \begin{equation} u_t(x,t) - u_{xx}(x,t) = 0 \text{ where $x\in\mathbb{R}$ and $t>0$} \end{equation}

And then a domain in the middle \begin{equation} u_t(x,t) - u_{xx}(x,t) = S \text{ where $x\in\mathbb{R}$ and $t>0$ and $S>0$} \end{equation}

And then a third right hand domain:

\begin{equation} u_t(x,t) - u_{xx}(x,t) = 0 \text{ where $x\in\mathbb{R}$ and $t>0$} \end{equation}

Boundary conditions are required at the start and end of the 1D line.

Are boundary conditions required between the domains, or can I just change the value of S to be nonzero in the middle and have no boundary conditions surrounding the central subdomain? If there are no central subdomain boundary conditions is the solutions approximately correct? Does the same principle apply to 2D and 3D pdes?

SPIL
  • 131
  • 3
  • 1
    You may want to apply some regularization as an enforced step change in partial derivatives can create unwanted effects between domains. – mathreadler Jun 25 '18 at 09:30
  • Hi mathreadler, thanks for the reply. Please can you recommend any books or weblinks on regularization. For a standard engineering problem, could the unwanted effects be severe or only minor? – SPIL Jun 25 '18 at 09:55
  • 1
    If not using any kind of regularization, then the effects can be catastrophic for any discrete solver. I am afraid I don't have any good book reference but I am sure there should exist many. – mathreadler Jun 25 '18 at 10:03
  • 1
    You could get equation system close to positive semi-definite and the solution in directions which are completely unrealistic could get norm growing completely out of control. – mathreadler Jun 25 '18 at 10:05
  • I forgot to add that the equation has discontinuous coefficients too. The software provides a converged solution, although the results are jagged between nodes is that a bad sign? Just because a software provides a converged solution, can the solution still be wrong? – SPIL Jun 26 '18 at 08:41
  • 1
    Yes if you miss regularization terms convergence can still give really unrealistic solutions. Imagine you try to solve an underdetermined system. There is then freedom for completely unregulated linear combinations to grow anywhere they want. – mathreadler Jun 26 '18 at 08:45
  • 1
    Maybe I can show example in answer some day after work. – mathreadler Jun 26 '18 at 08:55
  • Thks. The software does bound the variables. For example chemical concentration is forced to be positive. – SPIL Jun 26 '18 at 09:08
  • If the source term was a function of chemical reactions and these were changing at each point, would that be ok since the reactions are a function so part of the solved equations? Yes, an example would be useful, thanks. – SPIL Jun 26 '18 at 09:08
  • I have not simulated so many chemical reactions so I don't know so much what would be normal there. I added an example of regularization, but it got a bit too big for a comment. – mathreadler Jun 28 '18 at 06:15

1 Answers1

1

Note This is not intended to answer the question but to help understand the importance of regularization when solving differential equations using numerical schemes.

Assume we have a 2D grid with cartesian coordinates $(x,y)$ and for some reason we want to solve the function which minimizes the gradient of a scalar potential field $\phi(x,y)$ everywhere $$\min\int_\mathcal S \|\nabla \phi(x,y)\|_FdS$$ where dS is some small quadratic area element in $x$ and $y$. Given some boundary functions, say for example $\phi(x,y) = f(x,y)$ on $\mathcal C$.

Furthermore assume we make a discretization of our differential operators:

$$\nabla = \left[\frac \partial {\partial x},\frac \partial {\partial y}\right]^T : d_x = \left[\begin{array}{rr}1&-1\\1&-1\end{array}\right], d_y = \left[\begin{array}{rr}-1&-1\\1&1\end{array}\right]$$

finally we try to solve this with a big linear least squares problem:

$$\min\left\{\left\|\nabla \phi(x,y)\right\|_F^2+\left\|{\bf C}(\phi(x,y)-f(x,y))\right\|_F^2\right\}$$ Where C encodes the areas where the boundary function should hold (err.. the boundary, in other words).

Our first attempt, without any additional term, gives us a somewhat weird result..: (boundary areas $\mathcal C$ are inner circle and rectangular frame.)

enter image description here

We can see very visible chessboard patterns in the solution. However if we add a small regularizing term with filter $h = \left[\begin{array}{rr}-1&1\\1&-1\end{array}\right]$ we see we can get a much more naturally smooth solution:

enter image description here

mathreadler
  • 26,534
  • Thanks for sparing the time to clarify your comments. This is a useful demonstration. – SPIL Jul 01 '18 at 21:45