Taken from “Introduction to Linear Algebra” by Gilbert Strang:
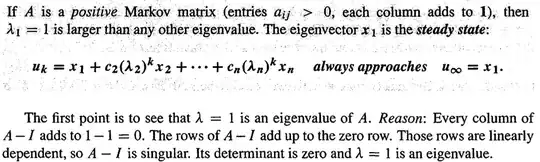
I can verify this property of Markov matrices through computation on example matrices, but can someone please provide clarity on the final statement that 1 is an Eigenvalue?
Taken from “Introduction to Linear Algebra” by Gilbert Strang:
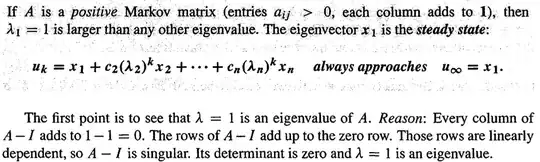
I can verify this property of Markov matrices through computation on example matrices, but can someone please provide clarity on the final statement that 1 is an Eigenvalue?
Since each column of $A$ sums to $1$, each column of $A-I$ sums to $0.$ This means that the sum of the rows (linear combination with coefficients all equal to $1$), is the $0$ vector. If there is a linear combination of row vectors with not all zero coefficients, then the rows are linearly dependent, and any matrix with linearly dependent rows (or columns) must have determinant $0.$ Thus, $\det(A-I) = 0,$ so by definition, $\lambda_1 = 1$ is an eigenvalue.
Edit: Recall that $\lambda$ is an eigenvalue of $A$ if and only if $Av = \lambda v$ for some nonzero vector $v.$ Rearranging, we can see that this statement is equivalent to $(A-\lambda I)v = 0.$ If $A-\lambda I$ is invertible, then $v = (A-\lambda I)^{-1} \cdot 0 = 0,$ which is a contradiction. So, we must have that $A-\lambda I$ is not invertible, i.e. $\det(A-\lambda I) = 0.$ Thus, an alternate definition is $\lambda$ is an eigenvalue of $A$ if and only if $\det(A-\lambda I) = 0.$ Since we have that $\det(A-1\cdot I) = 0,$ $\lambda = 1$ is an eigenvalue.
Let $c(t)=det(tI_n-A)$ be the characteristic polynomial of the given matrix. Then we need to show that $c(1)=0$.
We have $$c(1)=det\pmatrix{1-a_{1,1}&.&.&-a_{1,n} \\\\\\-a_{1,n}&.&.&1-a_{1,n}}$$. Now do $R_1\to R_1+R_2+...+R_n$, the determinant remains unchanged and the top row is zero.