Multiplication in permutation Group- cyclic

Question

In class I had to do this exercise:
$$ x = (1\, 3\, 6)\circ(1\,8\,9)\circ(3\,11)\circ(4\,12\,6\,5)=(1\,8\,9\,3\, 11\, 6\, 5\, 4\,12). $$ I do not understand how this result has been reached. Please if anyone can explain to me how it works if there are more than two cycles.

This will be helpful: https://math.stackexchange.com/questions/31763/multiplication-in-permutation-groups-written-in-cyclic-notation — user2345678, Jun 11 '18 at 12:00
Yes, I already read that. But I don't know how it works for more than 2 cycle — Mary, Jun 11 '18 at 12:02
I think the answer to the exercise is incorrect. Look for the right side of the equation, we got two number $1$ there, which cannot occur in this notation — user2345678, Jun 11 '18 at 12:03
Oh, i see. But anyway, I made a simpler version of this problem. Check it out — user2345678, Jun 11 '18 at 12:13
This also will be helpful: http://programathing.blogspot.com/p/multiplication-of-permutation-groups.html — user2345678, Jun 11 '18 at 12:23

score 2 · Answer 1 · answered Jun 11 '18 at 12:55

Let's ignore the fixed points and write this permutation in two-line notation: \begin{equation} x= \left(\begin{array}{cc} 1\ 3\ 6\ \\ 3\ 6\ 1\ \\ \end{array}\right) \left(\begin{array}{cc} 1\ 8\ 9\ \\ 8\ 9\ 1\ \\ \end{array}\right) \left(\begin{array}{cc} 3\ 11\\\ 11\ 3\\ \end{array}\right) \left(\begin{array}{cc} 4\ 12 \ 6\ 5\\\ 12\ 6\ 5\ 4\\ \end{array}\right). \end{equation}

Now, take each number, feed it in through these cycles from the rightmost cycle to the leftmost cycle and see what number gets outputted.

So, let's start with $1$. Observe that $1$ isn't in the first two cycles - then in the third one $1$ maps to $8$ and then $8$ doesn't appear on the top row of any further cycles. So the net result here is $1$ maps to $8$. So the cycle starts off with $(1\ 8$. We now proceed with $8$. We see that $8$ maps to $9$. Now our cycle looks like $(1\ 8\ 9$. Feeding $9$ in and we see that $9$ goes to $1$ and $1$ goes to $3$. So the net result here is that $9$ maps to $3$. So now we have $(1\ 8\ 9\ 3$. Proceed in this way for the remainder of the elements in the permutation and you will get the desired permutation $$(1\ 8\ 9\ 3\ 11\ 6\ 5\ 4\ 12).$$

this is the standard procedure of writing a permutation in 2 lines given its disjoint cycle notation. observe $$(a\ b\ c)\equiv\left(\begin{array}{cc} a\ b\ c\ \ b\ c\ a\ \ \end{array}\right).$$ — thesmallprint, Jun 11 '18 at 19:10

score 1 · Answer 2 · answered Aug 13 '18 at 08:48

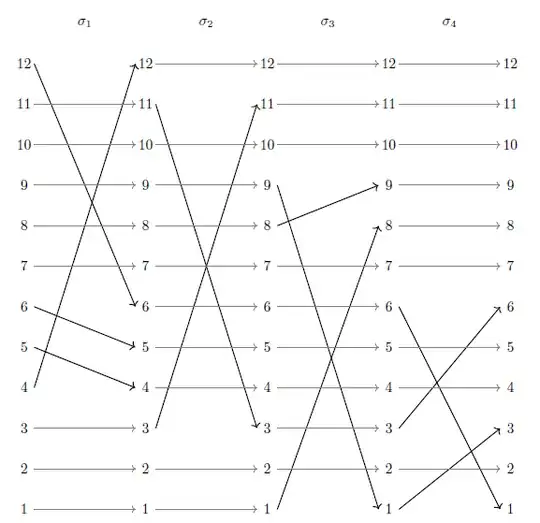
You may benefit from observing the diagrammatic version of permutations. Let's say that $$ \sigma_{1} = (4\quad 12\quad 6\quad 5),\quad \sigma_{2} = (3\quad 11),\quad \sigma_{3} = (1\quad 8\quad 9),\quad \sigma_{4} = (1\quad 3\quad 6). $$ In the case of $\sigma_{1}$, we understand this as $$ 4 \stackrel{\sigma_{1}}{\longmapsto} 12,\quad 12 \stackrel{\sigma_{1}}{\longmapsto} 6,\quad 6 \stackrel{\sigma_{1}}{\longmapsto} 5,\quad 5 \stackrel{\sigma_{1}}{\longmapsto} 4. $$ We also know that any other number $i$ maps to itself under $\sigma_{1}$, so $$ i \stackrel{\sigma_{1}}{\longmapsto} i\qquad\qquad \big(i \in \mathbb{N}\setminus\{4,5,6,12\}\big). $$ This means that the diagram associated to the product $\sigma_{4}\sigma_{3}\sigma_{2}\sigma_{1}$ is the following:

The order of the $\sigma_{i}$'s reflects the order in which we consider the permutations in the product. Finding the one-line cycle that corresponds to the product is now a simple case of following the lines!

For example, we have that $$ 1 \stackrel{\sigma_{1}}{\longmapsto} 1 \stackrel{\sigma_{2}}{\longmapsto} 1 \stackrel{\sigma_{3}}{\longmapsto} 8 \stackrel{\sigma_{4}}{\longmapsto} 8, $$ so that $1 \longmapsto 8$ in the product $\sigma_{4}\sigma_{3}\sigma_{2}\sigma_{1}$. I shall leave it to you to confirm the images of the other numbers.

Multiplication in permutation Group- cyclic

2 Answers2