Uniqueness of Solution to a Boundary Value Problem

Question

Question

Let $f:\mathbb R_+ \to \mathbb R_+$ be a function twice continuously differentiable (with derivative $f'$ and second derivative $f''$), and $a$, and $b$ be parameters in $\mathbb R_+$. Consider the system

\begin{align} \dfrac{dx(t)}{dt}=&\; f\left(x(t)\right)-y(t), \\[2ex] \dfrac{dy(t)}{dt}=&\; ay(t)\left(f'(x(t))-b\right), \end{align}

with $x(t)\ge 0$ and $y(t)\ge 0$ for all $t$, and boundary conditions

\begin{equation} x(0)= x_0, \qquad\text{and}\qquad\lim_{t\to\infty}e^{-bt}x(t)y(t)^{-a}=0. \end{equation}

By choosing $f$ appropriately it is possible to show that this system, without the initial condition, can have multiple stationary points. I would like to show, that even if that is the case, the following conjecture it true:

Conjecture $\;$ Given an $x_0$, there is a unique solution to the system that converges to one of the stationary points.

---

Why I think the conjecture is true

If $f'(0)>0$ and $f''(x)<0$ for all $x\in\mathbb R_+$, then there exists a unique stationary point and there is a simple proof of uniqueness of the solution given an arbitrary $x_0$ that involves drawing a phase diagram in the space $(x,y)$ and showing that there is a unique saddle path that the solution must be at all times (otherwise the second boundary condition would be violated) and that converges to the stationary point.

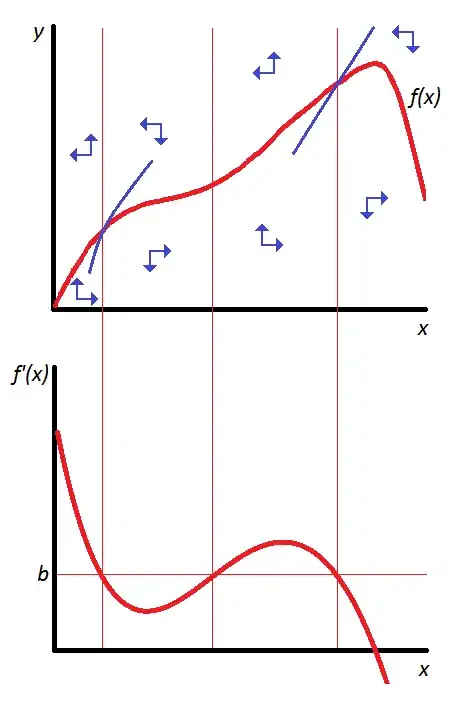
The reason why I think the conjecture is true is because, given an $f$ in $\mathcal C^2$, a similar phase diagram can be drawn. Here is a sketch of an example of a phase diagram with multiple stationary points:

Notice that the arrows flip between regions in a way that, given an $x_0$, there is only one saddle path (the lines in blue) that the solution could follow. My guess is that a proof for the conjecture would involve showing this is always the case.

---

Background

If $x$ denotes the capital stock, $y$ the consumption level, $f$ is the production function, $a$ the inverse of the intertemporal elasticity of substitution, and $b$ is the discount rate, then this system is describes the equilibrium allocation of a simple economic growth model.

Answer 1

Multiplying of the system equations leads to the equation in the form of $$\left(f(x(t))-y(t)\right)\dfrac{dy}{dt} = ay(t)\left(f'(x(t))-b\right)\dfrac{dx(t)}{dt}.\tag1$$ Presentation of the function $y(t)$ as the superposition $y(x(t)),$ $$\dfrac{dy}{dx} = \dfrac{y'_t}{x'_t}$$ allows to eliminate variable $t$ from $(1):$ $$(f(x)-y)\dfrac{dy}{dx} = ay\dfrac{d}{dx}(f(x)-bx).\tag2$$ Then $$(y-f(x))\dfrac{d}{dx}(y-f(x))+(y-f(x))f'(x)+ay(f'(x)-b)=0,$$ $$(y-f(x))\dfrac{d}{dx}(y-f(x))+((a+1)f'(x)-ab)y -f(x)f'(x)=0,$$ $$(y-f(x))\dfrac{d}{dx}(y-f(x))+((a+1)f'(x)-ab)(y-f(x))+a(f'(x)-b)f(x)=0.\tag3$$ Equation $(3)$ allows the substitution $$z(x)= y-f(x)\tag4,$$ $$\dfrac{dx}{dt}= -z(x(t)),$$ which changes the issue system to the form of \begin{cases} \dfrac{dt}{dx}= -\dfrac1z\\[4pt] z\dfrac{dz}{dx}+((a+1)f'(x)-ab)z+a(f'(x)-b)f(x)=0, \end{cases} \begin{cases} t= -\int\limits_{x_0}^x\dfrac{\,\mathrm d\xi}{z(\xi)}\\[4pt] \left(\dfrac{dz}{dx}+((a+1)f'(x)-ab)\right)z+a(f'(x)-b)f(x)=0.\tag5 \end{cases} Easy to see that the variable $t$ has the gaps in the points $x,$ where $z(x)= 0,$ or $y(x)=f(x).$

On the other hand, such points presents as the stationary points by the coordinate $t.$

Let us consider behavior of the equation $(5.2)$ at the simple case $$f(x)= cx+d,\quad s=h(cx+d).\tag6$$ Then $$zz'+(a(c-b)+c)z+a(c-b)(cx+d)=0,$$ $$\dfrac{dz}{dx}=\dfrac{dz}{ds}\dfrac{ds}{dx}= ch\dfrac{dz}{ds},$$ or $$z\dfrac{dz}{ds}+gz+s=0,\tag7$$ where $$\quad h = \sqrt{a\left(1-\dfrac bc\right)},\quad a(c-b)=ch^2,\quad g=h+\dfrac1h.\tag8$$ Equation $(7)$ has the common solution $$\begin{cases} \ln|z^2+gsz+s^2|-\dfrac{2g}{\sqrt{4-g^2}}\arctan \dfrac{2z+gs}{s\sqrt{4-g^2}}=c,\text{ if }|g|<2,\\ (s\pm z)\exp\dfrac{s}{s\pm z}=C,\text{ if }g=\pm2,\\ C_1|z-gs|^\alpha+C_2|z-gs|^\beta,\text{ if }|g|>2,\tag9 \end{cases}$$ wherein $$|C_1|+|C_2|>0,\quad \alpha,\ \beta = -\dfrac12\pm\dfrac12\sqrt{g^2-4}.\tag{10}$$ Exact solution $(9)-(10)$ has two branches. The reason is that the equation $(5.2)$ can be written in the form of $$\dfrac12\dfrac{dz^2}{dx}+((a+1)f'(x)-ab)\sqrt{z^2}+a(f'(x)-b)f(x)=0,$$ which allows existance of multiple solutions.