21

A medial magma is a set $M$ with a binary operation $*$ satisfying $$(a*b)*(c*d) = (a*c)*(b*d)$$ for all $a,b,c,d \in M$. Medial magmas constitute a finitary algebraic category $\mathsf{Med}$, therefore there is a functor $M : \mathsf{Set} \to \mathsf{Med}$ which sends a set $X$ to the free medial magma $M(X)$ over $X$. Elements of $M(X)$ can be seen as equivalence classes of oriented non-empty binary trees whose leaves are marked with elements of $X$, where two such trees are equivalent if the one can be reached from the other by a finite number of steps, where each steps looks as follows:

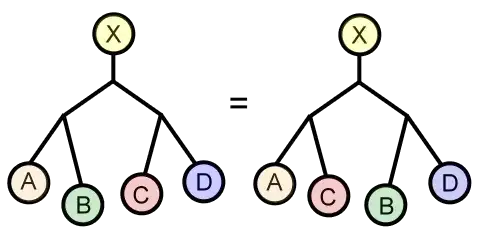
enter image description here

Now I wonder if there is a more explicit description of the underlying set of $M(X)$, or a specific system of representatives. Can we simplify it? For example, when $X=\{\star\}$, we have no markings; what is a specific system of representatives? I also wonder if these free medial magmas are studied or used anywhere in the literature.

Martin Brandenburg
  • 181,922
  • 3
    It seems that searching for "medial groupoid" instead of "medial magma" yields more results (in universal algebra groupoid is synonymous with magma). For instance, you can find the work of J. Ježek, T. Kepka and others who produced a number of papers on related structures and their representations, e.g. here (where the free cancellative and the free commutative medial magma are constructed) or here. – Martin Jan 06 '13 at 16:49
  • 1
    Thank you. In fact this gives more search results. But unfortunately I couldn't find a paper which discusses free medial groupoids. – Martin Brandenburg Jan 06 '13 at 22:42
  • 1
    Me neither. In the introduction to the second paper I linked there are a few remarks on free medial groupoids. There is something to the effect that "It seems that there is no very nice description of the equational theory of medial groupoids and free medial groupoids." I can only see the first two pages, so I don't know if there is more in later sections. – Martin Jan 06 '13 at 23:29
  • 1
    The commutative version has been studied under the name of "level algebras", see for example https://arxiv.org/pdf/math/0209363v3.pdf. – F. C. Apr 05 '20 at 08:23

0 Answers0