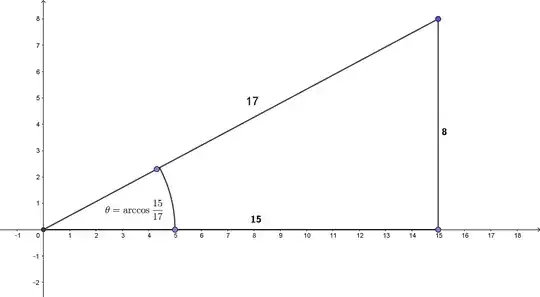
I had a simple thing to compute with a calculator: $$\sin\left(2\cos^{-1}\left(\frac{15}{17}\right)\right)$$ I got the decimal answer of about $0.83044983$, but when I typed it in WolframAlpha, it also gave an exact answer of $\frac{240}{289}$. How in the world would one get an exact answer here?
Asked
Active
Viewed 7,400 times
30
-
11Hint: $15^2+8^2=17^2$ – Prasun Biswas Mar 19 '18 at 21:38
-
@PrasunBiswas actually $8^2$ instead of $6^2$. I knew that, but still wasn't able to do it, because as it turns out i forgot about double angle formula – KKZiomek Mar 19 '18 at 21:40
-
8Hint #2: $2\times\dfrac 8{17}\times\dfrac{15}{17}=\dfrac{240}{289}$ – Prasun Biswas Mar 19 '18 at 21:41
-
how did this simple question get that many upvotes? – Deepesh Meena Aug 04 '18 at 17:45
-
@James I have no idea lol, I was thinking the same thing – KKZiomek Aug 08 '18 at 19:54
7 Answers
60
Here are three relevant formulas:
$\sin 2x = 2 \sin x \cos x$.
$\cos \cos^{-1} x = x.$
$\sin \cos^{-1} x = \sqrt{1 - x^2}$ after drawing an appropriate right triangle.
Combining these three to get the desired conclusion is left to the interested reader.
-
24My students don't reliably remember the condition on your second equality, so I'd recommend including it. ", if $-1 \leq x \leq 1$." – Eric Towers Mar 20 '18 at 15:13
-
1@EricTowers I might be one of those stupid students in this case, but if you allow complex numbers, doesn't that second equality hold? Or is there some multivalued function weirdness going on that you have to care about? – OmnipotentEntity Mar 20 '18 at 21:00
-
2Not "stupid" -- focusing on the "big", misremembering the "small". Since this Question is tagged "trigonometry", we're very likely talking about real-valued functions. The domain of real-valued arccosine is $[-1,1]$. (The usual extension to the complex plane has branch cuts along the rest of the real line. There is definitely some multivalued weirdness going on; cosine isn't injective, so this is unavoidable.) In fact, in Trig, any time a student uses the shortcut you write, they are expected to explicitly write that they have verified that $x$ is in the domain of arccosine. – Eric Towers Mar 21 '18 at 00:01
-
2@EricTowers: Arccos is multivalued, but for all possible values $y$ of $\cos^{-1}x$ you have $\cos y=x$, by definition. Thus, in complex numbers $\cos\cos^{-1}x=x$ is always true. The converse is not - you could have $\cos^{-1}\cos x\neq x$ if you chose the wrong branch. Whether students in a trig class should first show that $-1\le x\le1$, is more a question of pedagogy than mathematics. – Meni Rosenfeld Mar 21 '18 at 10:18
-
The same is with other inverse functions - for any branch of $\sqrt{x}$, you always have $\left(\sqrt{x}\right)^2=x$, but $\sqrt{x^2}$ can be either $x$ or $-x$ depending on $x$ and the branch. – Meni Rosenfeld Mar 21 '18 at 10:22
-
@MeniRosenfeld : I completely agree, for complex valued functions but not for real-valued functions. Which part of the Question or this Answer leads you to believe the asker or answerer is honestly considering complex-valued functions? – Eric Towers Mar 21 '18 at 16:32
-
@EricTowers: I was addressing primarily your remark that there is "multivalued weirdness", and wanted to emphasize it's not so weird in this case. – Meni Rosenfeld Mar 22 '18 at 00:16
-
@MeniRosenfeld : And I was echoing the Answerer's phrase "some multivalued function weirdness going on", without turning my comment into an Answer for a begged Question. – Eric Towers Mar 22 '18 at 15:09
-
@EricTowers: But the answer to OmnipotentEntity's (not the answerer) question "is there some multivalued function weirdness going on that you have to care about?" is "no", for the reason I mentioned. – Meni Rosenfeld Mar 22 '18 at 15:55
-
@MeniRosenfeld : I misremembered whose question it was; thanks for the correction. All the inverse trig functions are multivalued. I'm not going to disagree with someone about that fact's weirdness (without significantly more time/space to do so). While $\cos \cos^{1}( \cdots )$ hides multivaluedness, it does not eliminate the widespread error of applying functions outside their domains. At this point, I see your comment to be as confusing to the student who doesn't understand the restricted domain of arccosine as demonstrating to a Calc 1 class a solution to the equation $(fg)' = f'g'$. – Eric Towers Mar 22 '18 at 16:10
33
Call
$$ u = \cos^{-1}\frac{15}{17} $$
Therefore
$$ \cos u = \frac{15}{17} $$
and
$$ \sin u = \sqrt{1 - \cos^2 u} = \sqrt{1 - \frac{15^2}{17^2}} = \frac{8}{17} $$
With these two you just need to calculate
$$ \sin 2u = 2\sin u \cos u = 2\frac{15}{17}\frac{8}{17} = \color{blue}{\frac{240}{289}} $$
caverac
- 19,783
7
\begin{align} \sin \theta &= \dfrac{8}{17} \\ \cos \theta &= \dfrac{15}{17} \\ \hline \sin\left(2 \arccos \dfrac{15}{17} \right) &= \sin(2 \theta) \\ &= 2 \sin(\theta) \cos(\theta) \\ &= \cdots \end{align}
Steven Alexis Gregory
- 27,619
-
-
-
I didn't notice this answer before, but it deserves more points, I like that idea. If I could give two answers best answer, you would be the best answer too – KKZiomek Apr 18 '18 at 14:27
6
$ (8,15,17)$ are lengths of a Pythagorean triple right triangle. A narrow right triangle of these side lengths can be drawn if needed.
$$\sin(2\cos^{-1}\frac{15}{17}) = \sin(2\sin^{-1}\frac{8}{17}) = 2 \cdot \frac{8}{17}\cdot \frac{15}{17} =\frac{240}{289}.$$
Narasimham
- 42,260
3
Let $\cos^{-1}x=y\implies\cos y=x$
Using Principal values, $0\le x\le\pi\implies\sin y\ge0$
and $\sin y=+\sqrt{1-\cos^2y}=?$
Finally, $\sin2(\cos^{-1}x)=\sin2y=2\sin y\cos y=?$
lab bhattacharjee
- 279,016
3
Note that $$\sin\left(2\cos^{-1}(a)\right)=2\sin\left(\cos^{-1}(a)\right)\cos\left(\cos^{-1}(a)\right)=2a\sin\left(\cos^{-1}(a)\right)$$ and use the fact that $$\sin\left(\cos^{-1}\left(\frac{\text{adjacent}}{\text{hypotenuse}}\right)\right)=\frac{\text{opposite}}{\text{hypotenuse}}$$
TheSimpliFire
- 28,020
