I'm learning about gamma distribution. Any idea to derive gamma PDF? I am searching for a better intuition or a better sense to understand this function.
Note{ I understand how to integrate gamma function. I know that gamma distribution can be derived from exponential distribution, while exponential distribution can be derived from Poisson distribution, but I don't know how the process of derivation work.
Here are miscellaneous comments, perhaps you will find that some of them help your intuition.
Moment generating functions multiply. Suppose $X, Y \sim \mathsf{Exp}(1),$ independently. Then each random variable has MGF $m(t) = (1 - t)^{-1}.$ and the MGF of $T=X+Y$ is $$m_T(t) = m_X(t)m_Y(t) = (1 - t)^{-2},$$ which is the MGF of $T \sim Gamma(2,1).$
Means match. $E(X) = 1, E(Y) = 1, E(X + Y) = E(T) = 2.$ Suppose you are first in line waiting for service. The server takes an exponential length of time $X$ with $E(X) = 1$ to serve a customer (or the s/he serves customers at an average rate of 1 per minute). Because of the no-memory property of the exponential distribution, the time before you begin being served is $X.$ Then the length of time for you to be served is $Y,$ and the total time before you can be on your way is $T = X+ Y$ with $E(T) = 2.$
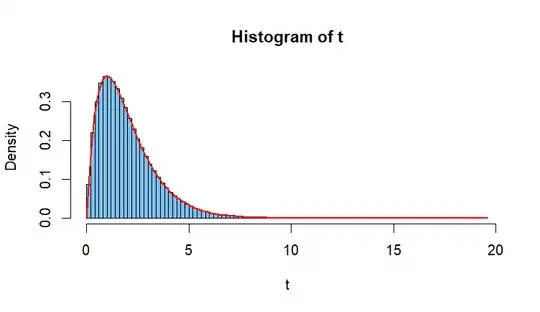
Simulation suggests distribution. Simulate a million sums $T,$ plot the histogram of these totals, and note that the pdf $f_T(x) = xe^{-x}$ for $x > 1,$ of $\mathsf{Gamma}(2,1)$ matches the histogram very well. (The code below is for R statistical software.)
x = rexp(10^6, 1); y = rexp(10^6, 1); t = x + y
hist(t, prob=T, br=100, col="skyblue2")
curve(x*exp(-x), 0, max(t), add=T, lwd=2, col="red")
Consider joint density. The joint density function of $X$ and $Y$ is $f_{X,Y}(x,y) = e^{-(x+y)},$ for $x, y > 0.$ Based on 100,000 of the pairs simulated above, the density of points plotted suggests the shape of the joint density function. The area beneath the diagonal green line includes the points for $P(T \le 3) \approx 0.8,$ which can be evaluated by an integral. More generally, you can integrate to find the CDF $F_T(x) = P(T \le x)$ and differentiate that to find the PDF $f_T.$
plot(x, y, pch=".", xlim=c(0,12), ylim=c(0,12), main="Scatterplot of (X, Y)")
abline(a=3, b=-1, col="green", lwd=2)
Notes: (1) Exponential and gamma distributions can be parameterized using either the mean/scale $\beta$ or the rate $\lambda = 1/\beta.$ (R uses the rate.) For simplicity here, I have chosen to use $\beta = \lambda = 1.$
(2) The sum of two exponential random variables is gamma only if the exponential random variables have the same rate (mean). Otherwise, the situation is somewhat messier mathematically and also less intuitive.
(3) This paper treats the case where $n$ exponentials are summed. You can set $n = 2$ when reading it. The case with different parameters is considered first, then the case with equal parameters.
