No: if $M$ is orientable and $N$ is not orientable (in particular, for the torus and the Klein bottle), then any covering $f:M\to N$ has even degree. Indeed, $N$ has an "orientation double cover" $\tilde{N}\to N$ (when $N$ is the Klein bottle this is just the 2-fold covering from the torus), and $f$ must be the composition of a covering map $M\to\tilde{N}$ with this double cover. If $N$ is orientable and $M$ is not orientable, then there are no covering maps $N\to M$ at all (any cover of an orientable manifold is orientable).
However, if $M$ and $N$ are closed connected orientable surfaces and $\chi(M)=p\chi(N)$ for some $p\in\mathbb{Z}_+$, then there exists a $p$-fold cover $M\to N$. When $M$ is orientable and $N$ is not, you can then apply this with the orientation double cover $\tilde{N}$ in place of $N$ to conclude that such a cover exists as long as $p$ is even (since $\chi(\tilde{N})=2\chi(N)$).
Here's a sketch of the proof. Let $N$ have genus $g$. If $g=0$, then $M$ must also have genus $0$, we must have $p=1$, and we can take our cover to be a homeomorphism. So suppose $g>0$, so $N$ is a connected sum of $g$ tori. Then $\chi(M)=p\chi(N)$ means $M$ has genus $p(g-1)+1$. Let us think of $N$ as one torus with $g-1$ tori attached to it, evenly spaced going around the first torus. Similarly, $M$ is one torus with $p(g-1)$ attached to it going around. We then get a $p$-fold cover $M\to N$ by just modding out the action of rotation by $2\pi/p$ on this picture (so every $(g-1)$st attached torus on $M$ becomes the same attached torus on $N$). Here is a picture of this in the case $g=2$ and $p=5$, taken from this nice answer to a similar question by Michael Albanese:
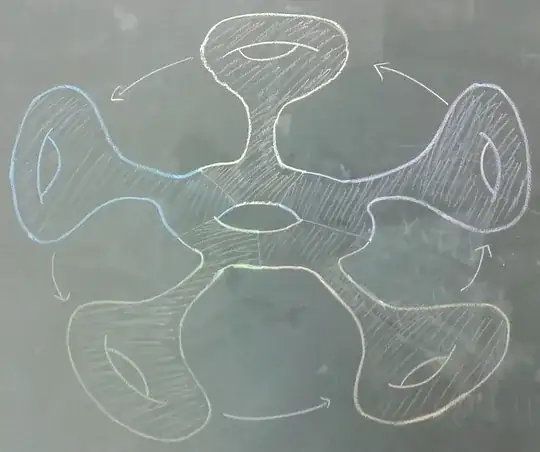
In the case $g=1$ (so $M$ and $N$ are just a torus), we can write this very explicitly. Thinking of $M=N=S^1\times S^1$ and $S^1\subset\mathbb{C}$ as the set of unit complex numbers, our map $f:S^1\times S^1\to S^1\times S^1$ is just $f(z,w)=(z^p,w)$. So, to get a covering of any even degree from the torus to the Klein bottle, you first use a map like this from the torus to itself, and then compose with the double cover from the torus to the Klein bottle.
I am not completely sure what you can say when $M$ and $N$ are both non-orientable. I believe that if $p$ is odd, you can do a construction similar to that above, except that instead of a torus in the middle of $M$ and $N$ you have a Klein bottle. I'm not sure you can get an even-degree cover between two non-orientable surfaces, though; this construction seems to need $p$ to be odd to be sure that the map on the Klein bottle in the middle is well-defined.
