Can a 'closed' curve be a function?

Question

For a 'closed' curve (I don't know if there is such in mathematics called closed curve, but I mean a curve which is 'closed')
e.g.1)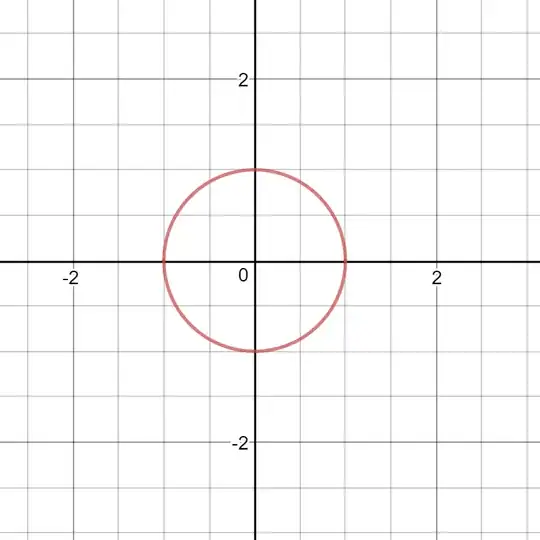It is well-known unit circle with equation$$x^2+y^2=1$$
e.g.2)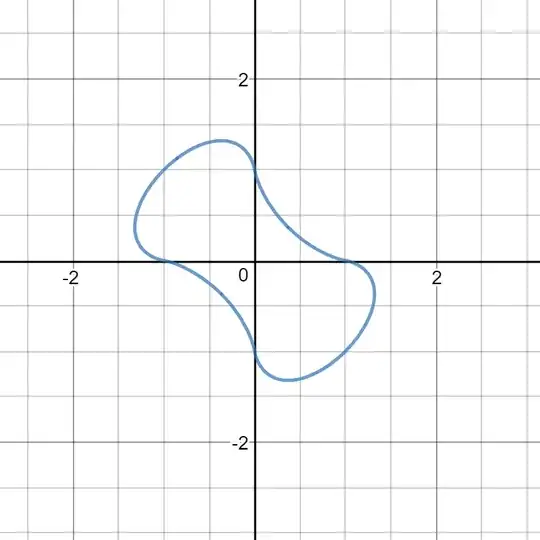It is the function $f$ which is in my another post.

I observed that they cannot be a function, since one $x$-value may correspond to several $y$-values, or will there be a 'closed' curve, such that one $x$-value can only correspond to at most one $y$-value, i.e., it is a function?

Answer 1

It cannot be the graph of a function $\mathbb{R} \rightarrow \mathbb{R}$ for the reason you stated: functions must have a unique output for a given input, and therefore their graphs must pass a "vertical line test". However, closed curves can be "graphs"$\mathbf{^\dagger}$ of functions $\mathbb{R} \rightarrow \mathbb{R}^2$. These are parametric functions (in two dimensions), which are of the form $f(t) = \langle x(t), \ y(t) \rangle$. For examples, the unit circle is given by $f(t) = \langle \cos(t), \sin(t) \rangle$ for $0 \leq t < 2\pi$ (technically this restriction on $t$ is unnecessary if you don't care about tracing it multiple times), and a line of slope $m$ passing through the origin can be parametrized as $f(t) = \langle t, mt \rangle$ for $-\infty \leq t \leq \infty$.

Notice that there's a fundamental difference in these graphs: the "ordinary" graphs that we're used to for functions $\mathbb{R} \rightarrow \mathbb{R}$ have an axis dedicated to the input variable, whereas the parametric plots have no visual representation for the input ($t$-value); both coordinates encode output information. Because of this, there is little restriction on how "graphs" of functions $\mathbb{R} \rightarrow \mathbb{R}^2$ can look. In particular, they do not have to adhere to the "vertical line test" and can be self-intersecting.

Moreover, as Mark Bennett points out in the comments, we can have closed curves arise as the graphs of polar equations, which have a reference angle, $\theta$ (w.r.t. the positive $x$-axis) as an input and a "distance from the origin" $r$ as an output. Because these graphs encode input data, they are not quite as free as parametric curves and must adhere to an analog of the "vertical line test": any ray with its tail at the origin cannot intersect the graph more than once for any $\theta$ in any given half-open interval of length $2\pi$, such as $[0, 2\pi)$. The need for this "interval addendum" is due to the fact that the inputs $\{ \theta + 2k\pi \ | \ k \in \mathbb{Z} \}$ for a given $\theta$ are "the same", graphically, despite actually being different.

Another common way of defining a curve is to select an appropriate set of conditions $\{P_k\}$ its points should satisfy (logical predicates) and do some set-building: $\{x \ | \ P_k(x) \text{ for all } k \}$. For instance, the unit circle is the collection of points $\{(x, y) \in \mathbb{R}^2 \ | \ x^2 + y^2 = 1\}$ or the collection of points $\{\mathbf{z} \in \mathbb{R}^2 \ | \ \mathbf{z} \text{ is 1 unit from (0,0)} \}$. Personally, I would hesitate to call what I'm looking at in this context a "graph", favoring instead terms like "locus of points" or possibly "algebraic curve", since we've merely given a description of the set of points instead of generating them by plugging inputs into a function. Though I guess you can get clever and take a predicate like $\{y \ | \ f(x) = y, \ x \in \mathbb{R} \}$ so that determining the locus is equivalent to the input/output process.

Enough semantics. The moral of the story here is that we need to specify both the domain and range of the functions to be considered and exactly what the coordinates on our graph paper represent.

---

$^\dagger$The reason for these quotes is that the term "graph", according to many mathematics texts (e.g. Wikipedia), refers specifically to the Cartesian plot of a set of ordered pairs $\{(x, f(x))\}$, i.e. a set of ordered pairs where each pair includes the function input. So when we plot the set of all outputs from a parametric function, what we get is not "graph" as such; rather, we are seeing a visual representation of the image of the function, and if the function is continuous, "parametric curve" or simply "curve" would probably be my preferred descriptor for the resulting shape, which at least agrees with Wikipedia's usage of that term.

Answer 2

A simple closed curve can't be the graph of a 1-variable function on $\mathbb{R}$. By the Jordan curve theorem, a closed curve partitions its complement into two parts, a bounded interior and an unbounded exterior. Pick any point in the interior and consider the vertical line through it. Since the interior is bounded both the ray on the line above the point and the ray below the point must leave the interior. The points where they leave correspond to failures of the vertical line test, hence the curve can't be the graph of a function.

Note that in the above proof, the vertical direction is somewhat arbitrary. The same basic argument shows that a simple closed curve can never be the graph of a function even after a rotation of axes. This contrasts with e.g. the case of parabolas. They can fail to be the graph of a function with respect to one choice of coordinate system , but you can always rotate the coordinate system so that the axis of symmetry of the parabola is parallel to the new y-axis (hence is the graph of a function with respect to that coordinate system). The fact that a simple closed curve is not the graph of a function is independent of coordinate system (you can clearly also translate the origin without changing anything essential in the argument).

Question: is the Jordan curve theorem equivalent to the statement that a simple closed curve is not the graph of a function with respect to any choice of coordinate system? If you knew this fact about simple closed curves, could you use it to prove the JCT?

Answer 3

A function transforms an object (number, vector...) in an object which is unique. With parametric functions it is absolutely the same :
For a given value of the parameter, $t$ for example, the image is unique. But between two images a relation may exist like it is the case with $cos t$ and $sin t$. On a graphical point of view the image $f(x)$ is unique is shown by the fact that for each point of the curve the ordinate is the unique image of a given absciss. So if $f$ is a function the curve which represents $f$ can't be closed. If you draw $f(x)=\cos x$ and $g(x)=\sin x$ you get two non closed curves because f and g are two functions of the variable x.
But if you draw the relation between $f$ and $g$ you get a closed curve because $f$ is not a function of the variable $g(x)$