Growth of the condition number of Hilbert matrices — theoretical vs Matlab

Question

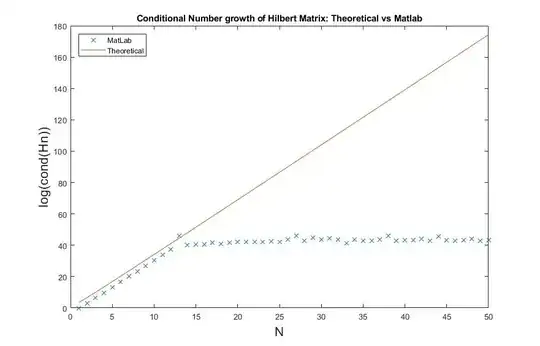
I need to investigate how the condition number of the Hilbert matrix grows with the size $N$. The Matlab command is cond(hilb(N),2):

1. Compute the condition number of the Hilbert matrices $H_N \in {\Bbb R}^{N \times N}$, for all $N \in \{ 1, 2, \dots, 50 \}$
2. Using Matlab to calculate the log of condition number of $H_N$ versus $N$. (The blue 'x')
3. Compare this with the anticipated theoretical growth (The red line) of $$O\left(\frac{(1+\sqrt{2})^{4N}}{\sqrt{N}}\right) $$

I got a plot like this:

When $N = 13$, the Condition Number reaches the maximum. The Condition Number does not continue to grow when $N>13$. Why does the Condition Number stop growing after $N=13$?

% generate Hilbert matrices and compute cond number with 2-norm
N=50; % maximum size of a matrix
condofH = []; % conditional number of Hilbert Matrix
N_it= zeros(1,N);
% compute the cond number of Hn
for n = 1:N
    Hn = hilb(n);
    N_it(n)=n;
    condofH = [condofH cond(Hn,2)];
end
% at this point we have a vector condofH that contains the condition
% number of the Hilber matrices from 1x1 to 50x50.
% plot on the same graph the theoretical growth line.
% Theoretical growth of condofH
x = 1:50;
y = (1+sqrt(2)).^(4*x)./(sqrt(x));
% plot
plot(N_it, log(y));
plot(N_it, log(condofH),'x', N_it,log(y));
% plot labels
plot(N_it, log(condofH),'x', N_it,log(y))
title('Conditional Number growth of Hilbert Matrix: Theoretical vs Matlab')
xlabel('N', 'fontsize', 16)
ylabel('log(cond(Hn))','fontsize', 16)
lgd = legend ('Location', 'northwest')
legend('MatLab', 'Theoretical')
legend('show')

Answer 1

In order to understand what exactly happens here, one has to take a close look at how the command cond is implemented in details, which I have not done (see the update at the end). However, one possible explanation for the phenomenon is the following: suppose you have to calculate the function $g(x)=x$, and the calculation is implemented as $g(x)=1/f(x)$ where $f(x)=1/x$. The function $g(x)$ has the linear growth (theoretically), but with floating point calculations for large $x$ (when $1/x$ becomes smaller than the MATLAB machine epsilon eps=$2^{-52}$) you will get round-off errors dominating in the denominator $$ g(x)\approx\frac{1}{\frac{1}{x}+{\rm eps}}\approx \frac{1}{{\rm eps}}\approx 2^{52}. $$ I guess that something similar happens in the command cond.

Update: After having a look at cond.m I confirm the phenomenon. MATLAB calculates the condition number for $p=2$ via SVD, that is, for Hilbert matrices it becomes $$ k(H_n)=\frac{\lambda_\max(H_n)}{\lambda_\min(H_n)}. $$ When $n\to\infty$ we have $\lambda_\max\to\pi$ (e.g. see this question) and $\lambda_\min\to 0$. Calculation with floating points for large $n$ looks as $$ k(H_n)\approx\frac{\pi}{\lambda_\min+{\rm eps}}\approx\frac{\pi}{\rm eps}\approx 2^{52}. $$

Answer 2

MatLab calculates Condition Number in this way:

$$Cond(H_n) = ||H_n^{−1}||⋅||H_n|| $$

One explanation for this is that MatLab uses: invhilb(n) to generate Hn-1. According to the MatLab documentation, invhilb(n) gives exact inverse of the Hilbert matrix without roundoff error when N<15. For N>=15, invhilb(n) involves round-off errors and Cond(Hn) Algorithm starts to loose robustness. This explains why Log(cond(Hn)) does not continue to grow after N=14.

For N>=15, I predict MatLab generates Hn-1 using inv(Hn) The documentation indicates that inv() performs an LU decomposition of Hn. Therefore this algorithm does round-off in $O(2/3N^3)$ times. It suffers from accumulation of roundoff errors.