Equivalent definition of a parabola as a locus of points given its focus and vertex

Question

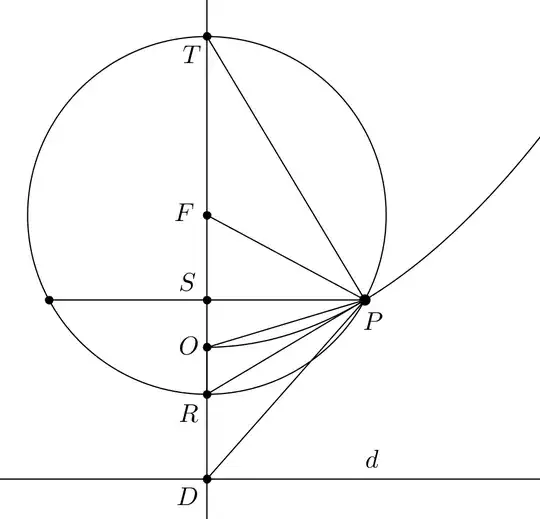
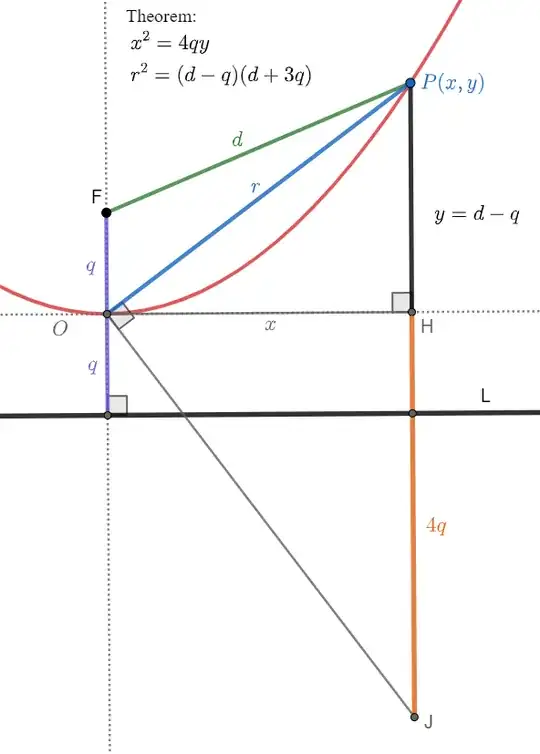
Consider the following alternative definition of a parabola:

Given two points $F$ and $O$ in the plane, the parabola having focus $F$ and vertex $O$ is the locus of points $P$ of the plane such that $$(FP - OF)(FP + 3 OF) = OP^2.$$

Using coordinates it is easy to see that the definition is equivalent to the usual one. Indeed, if we let $O = (0, 0)$, $F = (0, f)$ for some $f > 0$ and $P = (x, y)$, then the given equation simplifies to $x^2 = 4 f y$, which is precisely the equation of the parabola having focus $F$ and vertex $O$ as it is usually defined.

What I am interested in is a geometric proof that any parabola satisfies the above property, which should hopefully give some insight on why such an equality must hold. I have attempted to prove it in two ways:

1. As it is written, the equality seems to say that a certain rectangle (or maybe parallelogram?) has the same area as the square on the line segment $OP$. I have noticed that $FP - OF$ is the distance from $P$ to the tangent line to the parabola at $O$, but I don't know what to do with $FP + 3 OF$.
2. The equality can be rewritten as $$OP^2 + (2 OF)^2 = (FP + OF)^2.$$ Now it looks as though it could be proven using the Pythagorean theorem. But I haven't been able to draw a triangle having sides $OP$, $2OF$ and $FP+OF$ so that it can be seen that it is indeed a right triangle.

Any help would be highly appreciated.

(Background: this problem came up while trying to prove a similar property about the cissoid of Diocles, see this other question of mine. The two properties are related through inversion with respect to the unit circle centered at $O$.)

Answer 1

Let $D$ be the symmetric of $F$ with respect to $O$ and let $R$ be some point on the $OF$ line, such that $O$ lies between $F$ and $R$. Let $S$ be the symmetric of $R$ with respect to $O$. If the perpendicular to $OF$ through $S$ meets the circle centered at $F$ through $R$ at $P$, $P$ lies on the wanted parabola, since $PF=FR=SD$. Let $T$ be the symmetric of $R$ with respect to $F$ and let $OR=z$. Since $PO$ is a median in the right triangle $PSR$,

$$ PO^2 = \frac{2PS^2+2PR^2-SR^2}{4}=\frac{4PS^2+SR^2}{4}=PS^2+OR^2$$ but $PS^2 = RS\cdot ST = 2 OR\cdot ST$, hence $$ PO^2 = OR\left(OR+2ST\right)=(PF-OF)(2(OS+ST)-OR)$$ and $$ PO^2 = (PF-OF)(2OT-(PF-OF))=(PF-OF)(2(PF+OF)-(PF-OF))=(PF-OF)(PF+3OF).$$

Answer 2

This alternative definition of the parabola can be seen as a minor variant of the standard definition. Consider a parabola using the standard definition: given a focus $F$ and directrix $L$, let the parabola be the locus of points which are equidistant from $F$ and $L$. Drop a ⊥ from $F$ to $L$ and call the midpoint $O$ the vertex. By definition, it's on the parabola. Use $q$ to refer to the distance from $F$ to $O$ and from $O$ to $L$.

The normal thing to do is establish a coordinate system so that the origin is at $O$ and the $x$-axis is || to $L$. Take arbitrary point $P$ on the parabola, give it the coordinates $(x,y)$ and find a relationship between $x$, $y$, and $q$. Let $FP=PL=d$ so that $PH=y=d-q$ and $d=y+q$. Then $PF$ is the hypotenuse of a right triangle with legs $x$ and $y-q$ (not shown) so that: $$x^2 + (y-q)^2 = d^2 = (y+q)^2$$ $$x^2 + y^2 -2qy + q^2 = y^2 + 2qy + q^2$$ $$x^2 = 4qy$$ So far this is just the completely normal, standard way to derive and express the equation of the parabola relating $x$, $y$, and $q$. Most people do not attempt to interpret this equation geometrically, but this is possible using the figure above. Extend $PH$ past $H$ to point $J$ so that $HJ=4q$ as shown. $$x^2=4qy \implies \frac{x}{4q}=\frac{y}{x} \implies \frac{OH}{HJ}=\frac{PH}{OH} \implies \Delta PHO \sim \Delta OHJ$$ It then follows that $\angle POJ = 90^\circ$. We thus have a geometric analysis of the parabola leading to a geometric result (with a detour through some algebra). To me, this is a geometric proof, as you asked for above, because every element in the formula, $x$, $y$, and $4q$, is represented geometrically and can be understood geometrically. The takeaway is that if we construct the line at $O \perp$ to $OP$, it will meet line $PH$ at a point $J$ which is $4q$ below the $y$-axis.

Now to prove the formula from the question, we just observe that $$\Delta PHO \sim \Delta POJ \implies \frac{PH}{PO} = \frac{PO}{PJ} \implies \frac{y}{r}=\frac{r}{y+4q} \implies \frac{d-q}{r} = \frac{r}{d-q+4q}$$ $$\implies r^2=(d-q)(d+3q)$$

In other words, this formula just focuses on a different relationship among the three similar triangles which perhaps should have been our understanding of parabolas all along. Since this construction does "give some insight on why such an equality must hold", I think this answers the question. $x^2=4qy$ can be seen as the equation of the parabola for one who cares about the horizontal and vertical distances from the vertex to an arbitrary point. But $r$, $d$, and $q$ are perhaps more natural lengths to care about and this formula $r^2=(d-q)(d-q+4q)$ captures their relationship.