Pattern in Pascal's triangle

Question

Updated question

This "reverse" pattern can be plotted as a function of a triangle, read by rows:

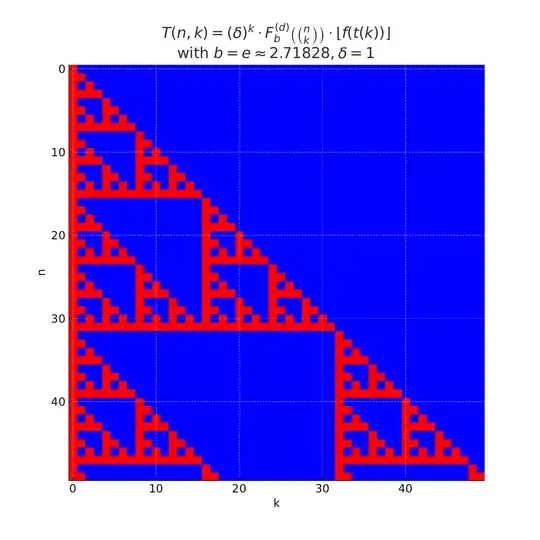
$$ T(n,k) = (\delta)^k F\binom{n}{k} \left\lfloor f(t(k)) \right\rfloor ,\delta\in\{1,-1\}.$$

The $T(n,k)$ here represents an "(alternating) transformation of Pascal's triangle":

• The $t(k)$ is the triangular numbers, to normalize the border of scatter plot to $y=x$.

• We can apply some border function $f(x)$, which gives a new border to the pattern.

• $F$ represents the transformation of the Pascal's triangle. The "reverse" transformation is given by $F := F^{(d)}_b(x)$: equals $1$ if the $d$th digit of $x$ is $1$ in base $b$, and $0$ otherwise.

• $\binom{n}{k}$ is the binomial coefficient, which makes up the Pascal's Triangle.

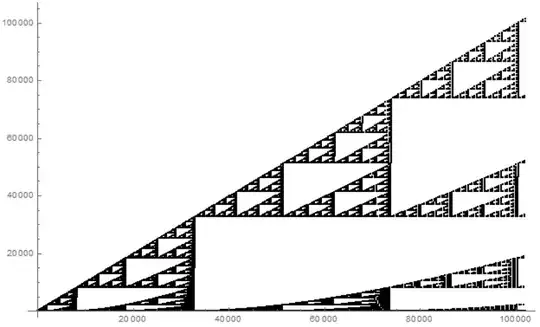
For example, here is the alternating ($\delta=-1$) "reverse pattern" with linear border $f(x)=x$, in number base $b=10$ for first digit case $d=1$: (Read $T(n,k)$ with described parameters by rows, and draw the terms as a scatter plot)

Or a similar example, but now $f(x)=\sqrt{x}$ (just the border changing example):

Question: How can we "explain" this pattern?

As of this update, my question boils down to: How can we describe these "arc" like, fractal like, patterns, in these plots of the "reverse/inverse" Pascal's pattern?

Can we relate them to similar structures, or "mathematically describe" and relate to some relevant results (theorems,...)?

Also, if we increase the base $b$, we get the "zooming in" effect. See gif at the end of the post.

For example, if the $F$ was the "normal Pascal's pattern (not reverse/inverse Pascal's pattern given above)", now given by taking the binomial coefficients modulo some prime number, then this pattern represents the Sierpiński triangle (also called Sierpiński gasket):

In this particular instance, we have $\delta=1$ and modulo $b=2$ for the now $F_b(x):=x \pmod b$ transformation (Instead of the $F^{(d)}_b(x)$ transformation), and linear ("outer") border $f(x)=x$.

The answer to "explain this pattern" in this case, was given in a similar question regarding this pattern. - It was related to the Lucas' theorem.

But my question here is, considering this new $F$ ("inverse") pattern - how can we "explain" it? - Like the "normal pattern" is "explained" by the fact that it gives a well known fractal, the Sierpiński triangle, and this process of converting the Pascal's triangle to the Sierpiński triangle, relates to Lucas's theorem.

---

---

---

Pre-update question contents

Known pattern

In general, numbers in pascals triangle produce sierpinski-triangl-like fractals. Some examples can be seen in this answer and are explained in this answer.

If we take the last digit of numbers (binomial coefficients) in the pascals triangle, and color the $\ne0$ digits white, we get the following image shown below; (First $1024$ rows)

Where this process is equivalent to taking $\binom{n}{k}\bmod m$ (where $m=10$ for this case) and coloring nonzero results. This is what was observed in the linked question/answers, for values of $m$ in general. (This is equivalent to taking last digit of binomial coefficients in some number base $m$)

Note that multiple patterns seem to be overlapping in the picture above. This is discussed in the linked answers. Only prime numbers $m$ produce clean patterns, and composite numbers like $10$ above are a combination of multiple prime patterns.

The pattern below does not care if number base (in context of first/last digit) is prime or not. It seems that, that variable in the pattern below, is used as a "zooming" factor to the picture of the pattern. See the gif at the end of the post.

---

"Reverse" pattern

But what if we take the first digit, instead of the last one, in some number base?

For decimal case, we have the following image, for comparison to the above: ($b=10$)

Where we colored the pixel if the first digit of the binomial coefficient is $"=1"$. (Since $0$ can't be the first digit) Similar pattern holds for any other single digit, in any other number base.

Why does this pattern appear in the pascals triangle, in all number bases?

Can it be somehow mathematically described or linked to any other things?

Like the first patterns links pascal triangle with sierpinski-triangle-like fractals, which can be explained for prime numbers by the Lucas' theorem (see linked answers) ?

You can observe the first $32$ number bases for the first $256$ rows: (10 images per second)

(Starting at base $3$ since in binary we have only one nonzero digit)

When the number bases are increasing, it looks like its "zooming into the tip".

You can also see the number base 3 compared to base 1000 .

Also see, that if we pick another digit $"= d"$ for our $"=1"$ condition, we get a "corrosed" effect on the pattern for bigger digits. See digits $1\dots9$ for $b=10$ example here as a gif.

---

Answer 1

well, the fact that you asked to link a pattern or a closed form that links both the triangle formation of yours through the transformation you mentioned as, $$ T(n, k) = (\delta)^k \cdot F^{(d)}_b\left( \binom{n}{k} \right) \cdot \left\lfloor f\left(t(k)\right) \right\rfloor $$ and then change the respective base values, and the value of delta oscillates or much better, changes from 1 and -1 based on different inputs in your so called " transformation" which turns to be really amazing that it can map the sierpinski triangle and some other beautiful fractals by changing its input function f(x). you also tried two combinations of it as square root of x and f(x)=x.

While your question is if there existed a new way of actually understanding or in a greater sense, "interpreting the inverse function and explaning it in a way"(till I understood it) has a answer very simple. The fact that changing the base of your function wont affect it as the values of delta only work on values of 1 and -1, and that only matters. This can be given by a simple visualization method by the pascal's triangle itself. consider the pascal's triangle as, $$ \begin{array}{cccccccccc} &&&&& \binom{0}{0} &&&& \\ &&&& \binom{1}{0} && \binom{1}{1} &&& \\ &&& \binom{2}{0} && \binom{2}{1} && \binom{2}{2} && \\ && \binom{3}{0} && \binom{3}{1} && \binom{3}{2} && \binom{3}{3} & \\ & \binom{4}{0} && \binom{4}{1} && \binom{4}{2} && \binom{4}{3} && \binom{4}{4} \\ \end{array} $$ and we now apply your transformation equation of $$ T(n, k) = (\delta)^k \cdot F^{(d)}_b\left( \binom{n}{k} \right) \cdot \left\lfloor f\left(t(k)\right) \right\rfloor $$ and this converts your standard pascal's triangle into something like, $$ \begin{array}{cccccccc} &&&&1&&& \\ &&&1&&1&& \\ &&1&&0&&1& \\ &1&&1&&1&&1 \\ 1&&0&&0&&0&&1 \\ \end{array} $$ which is nothing but the sierpinski triangle. But then you asked the question, "is there an other way of expressing this as the Lucas theorem for bionomial coefficients?" and for that question, I certainly do not have a good answer, but I would definitely try to find one, and I think it could also be given by changing the base values by actually introducing new values of delta, which might increase our chances of finding a new pattern. I also tried to fidget with some base values, and I tried it the Euler's constant e, and came up with the exact same representation as you did which was,

and also try other values for delta. I hope you find some new form for describing it.