A 2D Bézier curve is controlled by four 2D control points, say $\mathbf{P}_0$, $\mathbf{P}_1$, $\mathbf{P}_2$, $\mathbf{P}_3$. Its equation is
$$
\mathbf{P}(t) = (1-t)^3\mathbf{P}_0 + 3t(1-t)^2\mathbf{P}_1
+ 3t^2(1-t)\mathbf{P}_2 + t^3\mathbf{P}_3
\tag{1}\label{eq1}
$$
This is a "parametric" equation -- given a parameter value $t$ (which you can regard as time), this formula gives you a 2D point $\mathbf{P}(t)$. Writing $x$ and $y$ coordinates separately, the curve is
$$
x(t) = (1-t)^3 x_0 + 3t(1-t)^2 x_1 + 3t^2(1-t) x_2 + t^3 x_3
\tag{2}\label{eq2}
$$
$$
y(t) = (1-t)^3 y_0 + 3t(1-t)^2 y_1 + 3t^2(1-t) y_2 + t^3 y_3
\tag{3}\label{eq3}
$$
where $\mathbf{P}_i = (x_i,y_i)$ for $i=0,1,2,3$. This is the type of Bézier curve found in typical drawing programs or graphics packages. It's good for animating a point moving in 2D, but not very good for controlling movement in 1D.
Another approach would be to use an equation like \eqref{eq1} above to describe $y$ as a function of $x$:
$$
y(x) = (1-x)^3 y_0 + 3x(1-x)^2 y_1 + 3x^2(1-x)y_2 + x^3y_3
\tag{4}\label{eq4}
$$
We might call this a "functional" Bézier curve, as opposed to a parametric one.
Here, we don't have four control points, we have four control values, $y_0$, $y_1$, $y_2$, $y_3$. The functional form is less general, but it's quite suitable for use in animation: it gives you the "progress" $y(x)$ corresponding to a given time $x$.
So, how are the functional Bézier curve and the parametric one related? The answer is that the functional one is a special case of the parametric one. Suppose we substitute $x_0=0$, $x_1 = \tfrac13$, $x_2 = \tfrac23$, $x_3 = 1$
into equation \eqref{eq2} above. Then we get
$$
x(t) = (1-t)^3 (0) + 3t(1-t)^2 (\tfrac13) + 3t^2(1-t) (\tfrac23) + t^3 (1) = t
$$
So $x=t$, and equation \eqref{eq3} from above becomes
$$
y(t) = y(x) = (1-x)^3 y_0 + 3x(1-x)^2 y_1 + 3x^2(1-x)y_2 + x^3y_3
$$
which is the same as equation \eqref{eq4}.
So, in short, to get a Bézier function with control values $y_0$, $y_1$, $y_2$, $y_3$, we just need to construct a 2D Bézier curve with control points $\mathbf{P}_0 = (0,y_0)$, $\mathbf{P}_1 = (\tfrac13,y_1)$, $\mathbf{P}_2 = (\tfrac23,y_2)$, $\mathbf{P}_3 = (1,y_3)$.
For example, if you have the control values you mentioned: $u_0=0$, $u_1=0.05$, $u_2=0.25$, $u_3=1$, then the corresponding 2D control points are $(0,0)$, $(\tfrac13, 0.05)$, $(\tfrac23, 0.25)$, $(1,1)$.
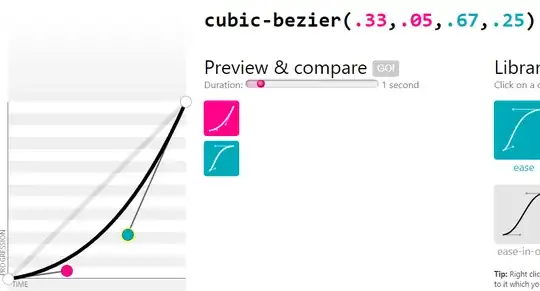
Conversely, suppose you have four control points $\mathbf{P}_0 = (0,0)$, $\mathbf{P}_1 = (x_1,y_1)$, $\mathbf{P}_2 = (x_2,y_2)$, $\mathbf{P}_3 = (1,1)$ describing a 2D Bézier curve, and you want to find the corresponding Bézier function. In general, this is not possible. In fact, it's only possible if
$x_1 = \tfrac13$ and $x_2 = \tfrac23$. And, in that case, the Bézier function defined by the control values $0, y_1, y_2, 1$ will give you the desired shape.
This causes lots of problems. Like here and here. People design a 2D Bézier curve, and then they want to use it as a function (i.e. they want to get the $y$ value corresponding to a given $x$). This is generally not possible (or, at least, it's not easy). If you want to control animation in 1D, I think you should use a function, not a 2D Bézier curve.
For example, suppose you try to find a function corresponding to the 2D curve with control points $\mathbf{P}_0 = (0,0)$, $\mathbf{P}_1 = (1,0)$, $\mathbf{P}_2 = (0,1)$, $\mathbf{P}_3 = (1,1)$. This curve looks like this:

You can't possibly represent this curve as the graph of a polynomial function (of any degree) because it has vertical slope at $x=\tfrac12$, which would never happen with a polynomial. If you want to use this curve for 1D animation, then you need to be able to calculate the $y$ value for a given $x$. In general, you will need to solve cubic equations to do this, which requires either nasty unstable formulas or numerical methods like Newton-Raphson. This particular example is very special because the relevant cubic is easy to solve, giving us:
$$
y = \frac{1}{48}(36 - 24x) + \frac34 (2x-1)^{1/3}
$$
But this is highly unusual; the solution of a cubic equation is typically a huge mess.

