28

I'm taking an online linear algebra course and got stuck with a problem (it's not for credit)... Since I don't know anyone qualified in person, this is last resort. Pretty sure I've made some trivial error, but can't find it... If you can spot it, please let me know. Thank you in advance.

As we know, absolute value of determinant of a square matrix is equal to the volume of the parallelepiped with edges corresponding to the matrix's columns (or rows).

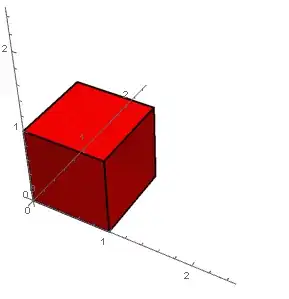
Consider matrix $A$ with columns $(1,1,0)^T,(0,1,1)^T,(1,0,1)^T$. Its determinant is 2. But it seems to me that the volume of the cube with edges corresponding to A's columns, is not 2… I mean, all three column vectors clearly have the same length, and it is $\sqrt2$, therefore volume of the cube with edges corresponding to these vectors must be $\sqrt2^3=2\sqrt2$.

What am I doing wrong?

Tim
  • 429

3 Answers3

58

The given vectors do not form a cube, so using the cube's volume formula is invalid. In particular, the vectors would need to be orthogonal (dot product zero for all pairs) for said formula to be applied, but here they are not. Indeed, the angle between each of the pairs here is 60°.

Parcly Taxel
  • 105,904
36

Your 3 vectors are related to a cube, but they do not form the cube edges. They are the diagonals of 3 adjacent faces:

enter image description here

Eric Duminil
  • 3,572
  • 7
    How did you make this animation? – mass Dec 04 '17 at 22:21
  • 9
    @SCarm: With SketchUp: Draw a cube. Remove the edges. Add color and trasnsparency to faces. Draw diagonals. Change background color and edge style. Hide axes. Define one scene with side view, another scene with Iso view. View > Animation > Play to check if it looks correct. File > Export > Animation > jpg to get 100 frames. convert -resize 800x600 -fuzz 1% -layers Optimize -delay 10 -loop 0 *.jpg animation.gif with imagemagick to get the animation. Have fun! – Eric Duminil Dec 05 '17 at 07:41
  • 1
    @EricDuminil JPEG?! Surely something lossless like PNG is better for converting to a GIF... Does SketchUp not support that? – wizzwizz4 Dec 05 '17 at 17:21
  • 1
    @wizzwizz4: You're right. The GIF was smaller with PNG's as input than with JPGS, without any -fuzz factor. Thanks for the comment! – Eric Duminil Dec 05 '17 at 21:32
26

I made a gif that shows the transformation. At the beginning you see the unit cube and at the end of the animation you see the unit cube as transformed by the matrix $$\begin{bmatrix}1 & 0 & 1\\ 1 & 1 & 0\\ 0 & 1 & 1\\\end{bmatrix}$$ As you stated this shape is not a cube but a parallelepiped so you can't calculate the area by multiplying the length of the spanning vectors. So what is the volume of this parallelepiped? There are a couple of ways to calculate this. It turns out the determinant of this matrix is one way, remembering that the determinant can be negative if the shape if flipped. This way is actually kind of tricky to proof for 3D matrices though. In two dimensions the determinant corresponds to the area of a parallelogram which you can proof geometrically.

Finally note that each unit vector gets mapped to their corresponding column vector in the matrix and that all parallel lines remain parallel. This helps you visualise matrix transformations. transformation gif

AccidentalTaylorExpansion
  • 1,736
  • 1
    "So what is the area of this parallelepiped? This is actually kind of complicated but the simplest way to calculate is given by the determinant of the matrix." Is it though? It's just (a x b) * c, where a, b, and c are the spanning vectors 'x' is cross product, and '*' is the dot product. – Shufflepants Dec 05 '17 at 20:01
  • You mentioned area but I keep thinking about the volume. Can't you calculate it by finding the area of one side multiplied by the remaining edge? Since the top side in this animation shows a parallelagram which happens to be two triangles that share a base the calc would be (1/2 base * height) * 2 or simply base * height, then multiply by the remaining edge $\sqrt2$? – Kelly S. French Dec 05 '17 at 20:30
  • @Shufflepants that's true, it still requires some work though to show the formula makes sense which I was going for. I modified my answer to make it less confusing. – AccidentalTaylorExpansion Dec 05 '17 at 21:42
  • @KellyS.French I meant volume, my bad. Remember that the height in your formula is $\sqrt 2 \cos 60^{\circ}$ since the two sides aren't perfectly perpendicular. For the same reason you don't multiply the area by $\sqrt 2$ but $\sqrt 2 \sin(\arcsin(\sqrt{2/3}))$ with $\arcsin(\sqrt{2/3})$ the angle between one side and the remaining edge. Sadly this isn't a nice angle but if you use the (a x b)*c formula for parallelepipeds you can calculate it nicely. – AccidentalTaylorExpansion Dec 05 '17 at 22:18
  • I might be a little out of my league but I enjoy learning so bare with me. As long as the top side is parallel to the bottom side, multiplying the area on the top by the distance between the top and bottom should still give the volume even if the angle of the height relative to the top side is skewed away from 90° because the angle of the height relative to the bottom side is a corresponding angle? Or is the area of the top not the same as the area of the bottom? That assumption is why I thought the height is still $\sqrt2$. Also, am I right about the area of the top? – Kelly S. French Dec 07 '17 at 01:53
  • @KellyS.French You are correct that you should multiply the area on the top by the distance between top and bottom. But because the top isn't exactly above the bottom, the distance (minimal distance between top and bottom) isn't $\sqrt 2$. Can you figure out the area of the top if you know the angle between vertices is $60^{\circ}$? – AccidentalTaylorExpansion Dec 07 '17 at 10:08
  • @user3502079 Yes, as long as the top is a parallelogram then it should be two triangles that share a base with a length of $\sqrt2$, the distance between the two closer corners. What I don't know is how to calculate the height, the distance between the two opposite corners that are farther apart; if I did then I wouldn't need to worry about the angles and it would be simply (1/2 B * H) * 2 or B * H, right? Is it obvious I'm avoiding Trig? ;) – Kelly S. French Dec 07 '17 at 17:14