What is a good way to explain why the graph of polynomials do not exhibit ripples, even in an arbitrarily small interval?

Question

I was showing someone the graph of $0.1x^9+0.6x^5+0.5x^2 + x$ on Wolframalpha (for this question, any real valued polynomial will do)

Someone asked me why the graphs of polynomials are smooth no matter what interval on $\mathbb{R}$ we look.

More precisely, the person asked me why there isn't random ripples like

or

as we travel along the graph of the polynomial.

Or using another example, imagine $x^2$, why isn't there a sinusoid like perturbation for this function in the range $(10000000018.3, 10000000019.1)$? A tinie tiny sinusoid?

My answer was basically that we can check the derivative and see that it is always going up or down. However, I am not totally satisfied with this answer.

So, what would be a good way to explain to someone why there isn't random oscillation (or ripples) in the interval (using another example, say) $(-398, -386)$ for the polynomial $x^{340} + 0.5x^{238} + 0.4x^{77} + 4$?

Answer 1

If $f$ is a degree $n$ polynomial then $f'$ is a degree $n - 1$ polynomial, and has at most $n - 1$ roots. That means that there can be at most $n - 1$ local maxima and minima of the function $f$. Likewise, this caps the number of changes in concavity.

This really strongly constrains the ripply behavior that you're talking about.

Answer 2

_{http://nbviewer.jupyter.org/gist/leftaroundabout/ce97d6e4023d206be638415b89694ca1}

The premise is flawed. I present to you $$ 2.2{x}^{1}-81.7{x}^{3}+1576.6{x}^{5}-12865{x}^{7}+53760.4{x}^{9}-128928.6{x}^{11}+185521.7{x}^{13}-158630{x}^{15}+74398.9{x}^{17}-14754.5{x}^{19}$$ As you see, this is much the same Gibbs phenomenon as you get with trigonometric functions. This phenomenon doesn't have so much to do with what precise basis functions you start with, as with how you determine the coefficients. Namely, a finite Fourier expansion of a function embeds the function in a Hilbert space, that is, a vector space of functions in which you have a scalar product that roughly tells you how similar two functions are. When you then pick some orthonormal basis, you can simply read off the coefficients for a given function by taking the scalar product with all the basis functions.

Concretely, the Fourier transform uses the $L^2$ space with the scalar product $$ \langle f,g\rangle_{L^2} = \int\limits_0^1\!\!\mathrm{d}x\:f(x)\cdot g(x) $$ That scalar product looks at the big picture, as it were, i.e. it classifies functions as similar if they give similar values over a large part of the interval $[0,1]$. It does not much care about fluctuations at any particular spot, and hence doesn't minimise these Gibbs oscillations.

This has nothing to do with the periodicity of the trig functions, and indeed you can easily find other functions that give an orthonormal basis on $L^2$. In the picture above, I've used the Legendre polynomials, which are orthogonal on $[-1,1]$.

The reason you see the Gibbs phenomenon more often explained with Fourier than with Legendre or other functions is that the Fourier basis is in some senses better conditioned. The coefficients of the Polynomial are quite big, and that is numerically a problem: everything gets unstable. Namely, if you evaluate the above approximation to the sawtooth only slightly outside the interval $[-1,1]$, the values diverge utterly from the target function:

Answer 3

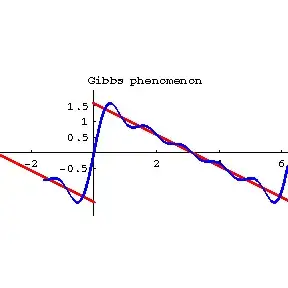
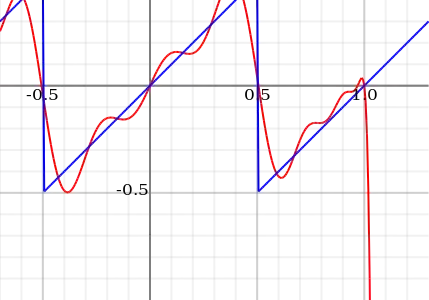
You seem to be trying to explain things to a non-mathematician, so I'm going to simplify my answer a bit and stop to explain things like the derivative. It's important to understand what these objects actually mean before we try to reason about them.

---

This is a somewhat deeper question than it may seem. It is entirely fair to ask why polynomials do not resemble (for example) the Weierstrass function when you zoom in on them.

The key property of the Weierstrass function is that it is continuous everywhere but nowhere differentiable. That is, it is defined everywhere and does not contain any sudden jumps, but you cannot draw a line tangent to any point on the graph, because it is too jagged for "tangent" to be a meaningful concept. The slope of such a tangent line would be called the derivative, but the Weierstrass function does not have a derivative.

Polynomials, on the other hand, are a special case of a family of functions known as the analytic functions. Analytic functions are functions which can be written in power series form, i.e. for some value $x_0$ and some sequence $a_n$, we have:

$$ f(x) = \sum_{n=0}^\infty a_n(x - x_0)^n $$

(The sum must converge, and the sum must specifically converge to $f(x)$. Otherwise we cannot say that one is equal to the other. Also, just for the purposes of this sum, we take the convention that $0^0 = 1$, so that the zeroth term of this series does not become undefined at $x = x_0$.)

A polynomial is an analytic function in which $a_n = 0$ for all $n$ greater than some number $d$, which we call the degree of the polynomial. You can also have analytic functions for which this is not true. Examples include the sine, cosine, and exponential functions, which all admit infinite series expansions.

As it turns out, each term of this sum is relatively easy to differentiate (find the derivative of), by first expanding and then applying the power rule. What makes the analytic functions special is that differentiating an analytic function gives us back another analytic function. As a result, every analytic function is infinitely differentiable; that is, we can keep taking derivatives as many times as we please.

But then, any wobbliness that the function might exhibit must eventually die down as we zoom in far enough. Otherwise, it would not be possible to draw a tangent line to it, and it would therefore lack a derivative. This also allows us to rule out (infinitely) many different kinds of larger-scale irregularities, such as sudden changes in concavity. Ruling out these irregularities is ultimately what allows the Taylor series formula to recover the power series of an analytic function using only information about a single point of the function's graph. The graph is so regular that a single point is all you need to extrapolate the whole.

Answer 4

What is a polynomial, really? It's a function that measures the product of the distances from $x$ to each of some fixed set of points. There's a convention for taking distance as negative or positive, depending which side of each point $x$ is on, and we might multiply by some constant to make the product uniformly bigger or smaller, but that's fixed for a given polynomial.

Now, distance is something that changes smoothly as $x$ moves along the number line. Sometimes, $x$ passes through one of the points, so the distance-product equals zero for an instant, but that's all that really happens.

With $f(x)=(x-2)(x-8)$, for example, there's not much story to tell. We start out with $x$ very far from both $2$ and $8$, then it gets close to $2$, passes through it, then gets close to $8$ and passes through it, then it gets far from both again. That's what a parabola is a picture of.

If you want a lot of little ripples, you would need a lot of points so that passing one and then another and then another causes the distance-product to change in a wiggly manner. With only a few points, the story just isn't that interesting.

(I haven't addressed polynomials with complex roots, but the only real difference there is that some of the points aren't on the number line at all, but off to the sides.)