5

I have made two prior posts regarding this concept, and it has evolved thanks to feedback and further clarification from this excellent community. I hope to provide a clear and simple presentation of its completed form, along with a new challenge to those interested.

A Prime Polygon is defined as a polygon where:

  1. Each vertex is assigned a unique value that is a multiple of 6. (e.g. 24, 36, 42, 120)
  2. The combined sum of all the vertices divided by 6 equals a prime number. (e.g. 37)
  3. When each of the vertices is added to this prime (e.g. 37), they each generate a new prime number. (e.g. 61, 73, 79, 157)

An example of a Prime Polygon:

Prime Polygon

Question & Challenge: Find a Prime Polygon with the largest number of vertices.

Bill Dubuque
  • 282,220
Tony
  • 943

2 Answers2

1

As it stands now, arbitrarily large examples are trivial to find.

{6, 12, 30, 42, 96} make a pentagon.

{6, 24, 30, 36, 60, 66} make a hexagon.

{12, 18, 36, 60, 78, 90, 96, 102, 132, 138, 150, 162, 222, 258, 276, 312, 330, 336, 342, 378, 396, 420, 432, 468, 498, 510, 522, 540, 552, 582, 588, 600, 630, 696, 708, 720, 732, 762, 876, 918, 948, 990, 1050, 1110, 1146, 1158, 1182, 1236, 1272, 1308, 1380, 1422, 1470, 1482, 1488, 1506, 1512, 1518, 1548, 1566, 1578, 1590, 1602, 1638, 1650, 1662, 1716, 1728, 1740, 1746, 1776, 1788, 1806, 1830, 1848, 1860, 1926, 1932, 1950, 1980, 1986, 1992, 2016, 2028, 2040, 2052, 2082, 2100, 2112, 2118, 2136, 2142, 2148, 2160, 2178, 2262, 2268, 2280, 2292, 2358} make a 100-gon.

Ivan Neretin
  • 13,429
  • Thanks! What do you mean by "trivial"? Would you change any of the conditions? – Tony Nov 14 '17 at 14:25
  • 1
    By trivial, I mean that one can find example for 5, then an example for 6, then think of a much larger number that would be remarkable in at least some way, come up with 100, and find that many, all that despite not being a math genius and having other job to do. As for change, it's not that simple. Now it's trivial; you change one tiny detail, and it becomes provably unsolvable. You change another tiny detail, and it becomes equivalent to a known open question. You change yet another, and it becomes so complicated that nobody would look at it. Inventing good problems is a tricky business! – Ivan Neretin Nov 14 '17 at 14:58
0

Let's look for the primes corresponding to a prime polygon, i.e., primes p which have an increasing partition (p1, ..., pN) (say, N >= 3), such that p + 6 pK is prime for each K = 1, ..., N.

The sum p = p1 +...+ pN ≥ N(N+1)/2, so N < sqrt(2p).

Since the parts are increasing, the largest possibility for the smallest part is when p2 = p1 +1, p3 = p1+2, ..., pN = p1+(N-1), so the sum is p = N*p1 + N(N-1)/2, whence p1 <= (p - N(N-1)/2)/N.

The largest part pN is largest when pK = K for K < N, then pN = p - N(N-1)/2

The second largest part must be less than pN, it is largest when the last two share about half of the maximum that remains after subtracting pK = K for K < N-1, viz. p[N-1] <= (p - (N-1)(N-2)/2 - 1) / 2. We can see how that generalizes: if I'm not wrong, we have p[N-i] ≤ (p - (N-i)(N-i-1)/2 - i*(i+1)/2)/(i+1) or p[i] ≤ (p - i*(i-1)/2 - (N-i+1)*(N-i)/2)/(N-i+1), but it actually doesn't really matter.

For the performance of the program, the most important is to use only numbers pK such that p + 6*pK is prime, and then, find a partition of the prime p into such parts.

is_pp(p, min_N=3)={for(N=min_N,sqrtint(2*p), /* make list of possible parts */
  my(PP=[],pK=1); until(#PP>=N && vecsum(PP[1..N-1])+PP[#PP] >= p,
    isprime(p+6*pK) && PP=concat(PP,pK); pK++); /* now find partition of p */
  forvec(ii=vector(N-1,i,[1,#PP-1]), my(pp=vecextract(PP,ii), pN=p-vecsum(pp));
    pN > pp[#pp] && setsearch(PP,pN) && return(concat(pp, pN))
  , 2))}

forprime(p=2,99,print1(p": " if(P=is_pp(p),P,"nope") ", ")))
2: nope, 3: nope, 5: nope, 7: [1, 2, 4], 11: [1, 2, 8], 13: [1, 3, 9], 
17: [1, 2, 14], 19: [2, 3, 14], 23: [1, 3, 19], 29: [2, 3, 24], 31: [1, 2, 28], 
37: [1, 4, 32], 41: [1, 2, 38], 43: [3, 9, 31], 47: [1, 2, 44], 53: [1, 3, 49], 
59: [2, 7, 50], 61: [1, 2, 58], 67: [1, 5, 61], 71: [2, 3, 66], 73: [1, 11, 61], 
79: [3, 8, 68], 83: [1, 3, 79], 89: [2, 3, 84], 97: [1, 2, 94], ..


forprime(p=1,99,print1(p": "if(P=is_pp(p,4),P,"nope")", ")) \ squares
2: nope, 3: nope, 5: nope, 7: nope, 11: [1, 2, 3, 5], 13: [1, 3, 4, 5], 
17: [1, 2, 5, 9], 19: [2, 3, 4, 10], 23: [1, 3, 4, 15], 29: [2, 3, 4, 20], 
31: [1, 2, 6, 22], 37: [1, 4, 5, 27], 41: [1, 2, 3, 35], 43: [3, 4, 5, 31], 
47: [1, 2, 7, 37], 53: [1, 3, 5, 44], 59: [2, 4, 5, 48], 61: [1, 2, 6, 52], 
67: [1, 2, 5, 59], 71: [2, 3, 6, 60], 73: [1, 4, 14, 54], 79: [3, 4, 8, 64], 
83: [1, 3, 8, 71], 89: [2, 3, 4, 80], 97: [1, 2, 5, 89], ...


forprime(p=1,99,print1(p": ",if(P=is_pp(p,5),P,"nope"),", ")) \ pentagons
2: nope, 3: nope, 5: nope, 7: nope, 11: nope, 13: nope, 17: nope, 19: nope, 
23: [1, 3, 4, 5, 10], 29: [2, 3, 4, 7, 13], 31: [1, 2, 5, 7, 16], 
37: [1, 4, 5, 6, 21], 41: [1, 2, 3, 10, 25], 43: [3, 4, 5, 6, 25], 
47: [1, 2, 4, 6, 34], 53: [1, 3, 5, 6, 38], 59: [2, 4, 5, 9, 39], 
61: [1, 2, 3, 7, 48], 67: [1, 2, 5, 7, 52], 71: [2, 3, 5, 6, 55], 
73: [1, 4, 5, 9, 54], 79: [3, 4, 5, 8, 59], 83: [1, 3, 4, 5, 70], 
89: [2, 3, 4, 8, 72], 97: [1, 2, 5, 9, 80], ...

(This prints the values of the vertices divided by 6.)

So it seems that for all primes >= 1+2+3 (minimum required to get a polygon, i.e., >= 3 vertices, with distinct values at the vertices), there is a prime triangle, most often even with two vertices having values <= 3*6. Similar for prime squares and prime pentagons, and probably all other number of vertices. Let's look at the smallest prime n-gon: (not sure these are the smallest, for each n I don't try smaller p's)

p=7;for(n=3,20,while(!P=is_pp(p,n),p=nextprime(p+1));print("Prime "n"-gon with p = "p": parts = "P))
Prime 3-gon with p = 7: parts = [1, 2, 4]
Prime 4-gon with p = 11: parts = [1, 2, 3, 5]
Prime 5-gon with p = 23: parts = [1, 3, 4, 5, 10]
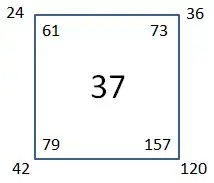
Prime 6-gon with p = 37: parts = [1, 4, 5, 6, 10, 11]
Prime 7-gon with p = 41: parts = [1, 2, 3, 5, 7, 8, 15]
Prime 8-gon with p = 61: parts = [1, 2, 3, 6, 7, 8, 11, 23]
Prime 9-gon with p = 83: parts = [1, 3, 4, 5, 8, 9, 11, 14, 28]
Prime 10-gon with p = 97: parts = [1, 2, 5, 7, 9, 10, 11, 14, 16, 22]
Prime 11-gon with p = 127: parts = [2, 4, 5, 6, 9, 11, 12, 14, 16, 17, 31]
Prime 12-gon with p = 139: parts = [2, 3, 4, 7, 9, 10, 12, 14, 15, 17, 22, 24]
Prime 13-gon with p = 167: parts = [1, 2, 4, 5, 10, 11, 12, 14, 15, 16, 17, 21, 39]
Prime 14-gon with p = 227: parts = [1, 2, 4, 5, 6, 7, 9, 11, 14, 15, 20, 21, 26, 86]
Prime 15-gon with p = 227: parts = [1, 2, 4, 5, 6, 7, 9, 11, 14, 15, 20, 21, 22, 29, 61]
Prime 16-gon with p = 227: parts = [1, 2, 4, 5, 6, 7, 9, 11, 14, 15, 20, 21, 22, 26, 27, 37]
Prime 17-gon with p = 307: parts = [1, 4, 5, 7, 10, 11, 12, 15, 17, 19, 21, 22, 25, 26, 30, 32, 50]
Prime 18-gon with p = 347: parts = [1, 2, 6, 7, 9, 12, 14, 16, 17, 19, 20, 22, 24, 26, 27, 29, 37, 59]
Prime 19-gon with p = 383: parts = [1, 3, 6, 8, 10, 11, 13, 14, 16, 18, 20, 21, 23, 29, 30, 31, 34, 35, 60]
Prime 20-gon with p = 419: parts = [2, 4, 5, 7, 8, 10, 12, 14, 15, 17, 23, 24, 25, 28, 29, 30, 33, 37, 39, 57]

This takes less than 0.1 second. Similarly, to find the first 30-, 40- ... gon:

Prime 30-gon with p = 1091: parts = [1, 2, 3, 10, 12, 15, 16, 17, 21, 22, 23, 28, 31, 32, 33, 35, 36, 38, 45, 46, 47, 53, 56, 57, 58, 60, 65, 66, 67, 96]
Prime 40-gon with p = 2063: parts = [1, 3, 4, 6, 8, 11, 13, 15, 24, 25, 29, 30, 34, 35, 39, 41, 45, 46, 48, 49, 53, 55, 56, 58, 59, 60, 63, 64, 66, 69, 78, 80, 81, 86, 88, 91, 93, 95, 99, 163]
Prime 50-gon with p = 3163: parts = [1, 3, 4, 9, 11, 15, 16, 18, 23, 24, 25, 26, 28, 30, 33, 35, 38, 45, 49, 50, 51, 56, 58, 59, 61, 63, 64, 66, 68, 70, 74, 75, 78, 79, 80, 85, 88, 89, 91, 94, 95, 96, 101, 105, 110, 114, 115, 119, 126, 250]
Prime 60-gon with p = 4919: parts = [2, 3, 4, 8, 9, 14, 15, 17, 20, 22, 27, 28, 30, 38, 39, 42, 45, 52, 53, 57, 59, 60, 63, 64, 65, 69, 72, 77, 78, 79, 80, 83, 87, 92, 93, 94, 97, 98, 100, 102, 109, 112, 120, 122, 123, 125, 129, 132, 133, 137, 144, 147, 148, 149, 154, 155, 157, 158, 160, 168]
Prime 70-gon with p = 7433: parts = [3, 4, 8, 9, 11, 14, 15, 16, 18, 19, 21, 24, 25, 26, 29, 35, 36, 40, 43, 45, 49, 54, 60, 64, 65, 66, 68, 70, 74, 75, 78, 79, 81, 84, 86, 96, 101, 106, 108, 109, 110, 113, 114, 115, 119, 123, 131, 133, 134, 135, 140, 143, 144, 155, 156, 159, 165, 166, 169, 178, 180, 184, 185, 190, 194, 196, 199, 205, 208, 876]
Prime 80-gon with p = 9137: parts = [4, 6, 11, 12, 14, 15, 17, 20, 24, 26, 29, 31, 34, 39, 40, 46, 47, 49, 50, 54, 55, 56, 57, 59, 60, 64, 66, 67, 69, 75, 81, 82, 90, 92, 97, 101, 102, 105, 109, 111, 116, 117, 119, 120, 125, 131, 132, 134, 145, 150, 154, 155, 157, 159, 161, 166, 167, 169, 171, 172, 174, 176, 179, 181, 185, 186, 187, 189, 192, 194, 196, 199, 200, 201, 209, 215, 216, 220, 227, 325]
Prime 90-gon with p = 11777: parts = [1, 2, 4, 5, 6, 9, 15, 20, 21, 22, 25, 26, 27, 32, 34, 35, 39, 44, 49, 54, 55, 56, 57, 61, 62, 64, 70, 71, 75, 77, 79, 81, 82, 84, 91, 92, 95, 100, 104, 106, 110, 116, 117, 119, 120, 121, 125, 127, 132, 139, 144, 145, 146, 147, 149, 152, 156, 161, 169, 172, 174, 186, 187, 189, 190, 191, 194, 196, 197, 201, 204, 205, 210, 211, 212, 221, 222, 224, 225, 229, 231, 235, 240, 242, 244, 247, 256, 259, 265, 691]
Prime 100-gon with p = 14489: parts = [5, 8, 9, 10, 12, 17, 22, 23, 24, 25, 28, 30, 35, 38, 39, 42, 43, 44, 45, 47, 49, 54, 57, 59, 63, 65, 67, 68, 75, 77, 78, 80, 88, 94, 98, 99, 102, 103, 107, 108, 110, 112, 114, 123, 124, 129, 130, 133, 135, 140, 145, 148, 149, 152, 154, 159, 162, 163, 164, 168, 173, 177, 180, 182, 190, 192, 193, 197, 199, 207, 208, 210, 212, 213, 214, 217, 218, 219, 220, 232, 233, 239, 245, 247, 252, 253, 262, 263, 264, 267, 268, 269, 273, 275, 283, 284, 288, 289, 322, 409]
Max
  • 484