3

[Major Revision 11/13/2017 1:00 AM]

My original post presented the concept of a "Prime Square". The conditions were obviously lacking as the user PM 2 Ring was able to discover 13544 combinations under 2000.

I have since updated the criterion to reflect a popular post I made in the past: Sets of Prime and Composite Numbers

This is an example of the updated concept:

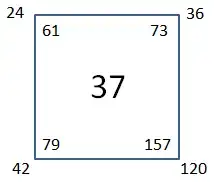
enter image description here

$ 24 + 36 + 42 + 120 = 222 $

$ 222 / 6 = 37 $

$ (37 + 24) = 61 ; (37 + 36) = 73 ; (37 + 42) = 79 ; (37 + 120) = 157 $

Definition: Each corner represents the average of one of the four possible sets, with no set appearing more than once. If their sum (222) divided by 6 equals a prime, and furthermore that prime(37), when added to each of the four corners, equals four new primes (61, 73, 79, 157), then it's a Super Prime Square.

The sets are as follows:

We know that all primes are of the form $ 6k ± 1 $ with the exception of 2 and 3.

We also know that not all numbers of the form $ 6k ± 1 $ are prime.

This leads to four distinct sets of pairs adjacent to a multiple of six:

  1. Twin Primes, Example: $ 5, 7 $ (prime followed by a prime)
  2. Twin Composites, Example: $ 119, 121 $ (composite followed by a composite)
  3. Prime-Composite, Example: $ 23, 25 $ (prime followed by a composite)
  4. Composite-Prime, Example: $ 35, 37 $ (composite followed by a prime)

Question: The challenge is to find the largest Super Prime Square such as [42, 24, 36, 120] 37; that when the solution (such as 37) is added to each of the four corners yields four new primes ( 79, 61, 73, 157)

Thanks!

Tony
  • 943
  • 1
    why don't you try to find such numbers starting from a given prime p, then see if you can divide 6p into 4 distinct composite numbers all multiple of 6? – user25406 Nov 11 '17 at 20:44
  • @user25406 It can't just be 4 distinct composite numbers because each of the four needs to belong to one of the four sets I described. In other words, each of the four needs to be represented, the set cannot repeat. – Tony Nov 11 '17 at 20:49
  • 1
    I think you should expound more. Sounds interesting – Daniel Donnelly Nov 11 '17 at 23:20
  • Another Prime Square is 18 + 84 + 78 + 186 = 366 ; 366 / 6=61 ; 61 is Prime – Tony Nov 12 '17 at 04:19
  • 1
    Seems that we can get any prime $p\ge 31$ and that there are plenty of quartuples doing the job. Upto the prime $631$, there are multiple solutions (except for $p=31$) – Peter Nov 12 '17 at 10:45
  • 1
    The $5$ solutions for $p=37$ are : [12, 24, 66, 120] 37 [12, 54, 36, 120] 37 [18, 24, 36, 144] 37 [18, 48, 36, 120] 37 [42, 24, 36, 120] 37 – Peter Nov 12 '17 at 10:50
  • 1
    And the $9$ solutions for $p=41$ are : [6, 24, 96, 120] 41 [6, 54, 66, 120] 41 [6, 84, 36, 120] 41 [12, 24, 66, 144] 41 [12, 48, 66, 120] 41 [12, 54, 36, 144] 41 [18, 48, 36, 144] 41 [42, 24, 36, 144] 41 [42, 48, 36, 120] 41 – Peter Nov 12 '17 at 10:53
  • @lurker what do you mean by is there a sequence of numbers $31$ that fit this criterion? – Daniel Donnelly Nov 12 '17 at 19:00
  • @Peter Thanks for the feedback! I've since updated the challenge! – Tony Nov 13 '17 at 06:10
  • @EnjoysMath My challenge has been updated to reflect recent revelations from feedback. I'm now only interested in the highest value of this new concept. – Tony Nov 13 '17 at 06:16
  • 1
    @lurker I suggest to name the desired prime-squares "super-prime-squares" – Peter Nov 13 '17 at 09:38

1 Answers1

3

Here the PARI/GP code for the search of super-prime-squares (having the additional desired property) and an already large example. 

? gef=0;while(gef==0,a=random([100,10^6]);while(1-(Mod(a,6)==0)*(isprime(a-1,2)=
=1)*(isprime(a+1,2)==1),a=random([100,10^6]));b=random([100,10^6]);while(1-(Mod(
b,6)==0)*(isprime(b-1,2)==0)*(isprime(b+1,2)==1),b=random([100,10^6]));c=random(
[100,10^6]);while(1-(Mod(c,6)==0)*(isprime(c-1,2)==1)*(isprime(c+1,2)==0),c=rand
om([100,10^6]));d=random([100,10^6]);while(1-(Mod(d,6)==0)*(isprime(d-1,2)==0)*(
isprime(d+1,2)==0),d=random([100,10^6]));p=vecsum([a,b,c,d])/6;if(isprime(p,2)==
1,if(isprime([a,b,c,d]+vector(4,j,p),2)==[1,1,1,1],gef=1)));print([a,b,c,d],"
",p,"     ",[a,b,c,d]+vector(4,j,p))
[155862, 377346, 449400, 511314]   248987     [404849, 626333, 698387, 760301]
?

Here an example with $10$-digit numbers (one of the sums has even $11$) :

[7930195380, 5831272896, 4808600274, 1846715928]   3402797413     [11332992793,
9234070309, 8211397687, 5249513341]
Peter
  • 86,576