Does the "prime ant" ever backtrack?

Question

A few mathematical questions have come up from the question "The prime ant " on the Programming Puzzles & Code Golf Stack Exchange.

Here is how the prime ant is defined:

Initially, we have an infinite array A containing all the integers >= 2 : [2,3,4,5,6,.. ]

Let p be the position of the ant on the array. Initially, p = 0 (array is 0-indexed)

Each turn, the ant will move as follows:

if A[p] is prime, the ant moves to the next position : p ← p+1

else, if A[p] is a composite number, let q be its smaller divisor > 1. We divide A[p] by q, and we add q to A[p-1]. The ant moves to the previous position: p ← p-1

Here are the first moves for the ant:
 2  3  4  5  6  7  8  9  ... 
 ^
 2  3  4  5  6  7  8  9  ... 
    ^
 2  3  4  5  6  7  8  9  ... 
       ^
 2  5  2  5  6  7  8  9  ... 
    ^
 2  5  2  5  6  7  8  9  ... 
       ^
 2  5  2  5  6  7  8  9  ... 
          ^
 2  5  2  5  6  7  8  9  ... 
             ^
 2  5  2  7  3  7  8  9  ... 
          ^

Questions relate to proving the sequence is well-defined:

I wonder whether the sequence is well-defined for arbitrarily large n (or whether the composite case could ever push the ant to the left of the initial 2). – Martin Ender♦ Oct 9 at 6:59

Whether all prime values appear:

@MartinEnder Another open question is whether a prime > 7 can eventually be left behind for good. – Arnauld Oct 9 at 10:39

And what the asymptotic growth looks like:

@Arnauld I'm curious how the ant's position grows with respect to the number of moves. My guess is logarithmic. – kamoroso94 Oct 9 at 12:58

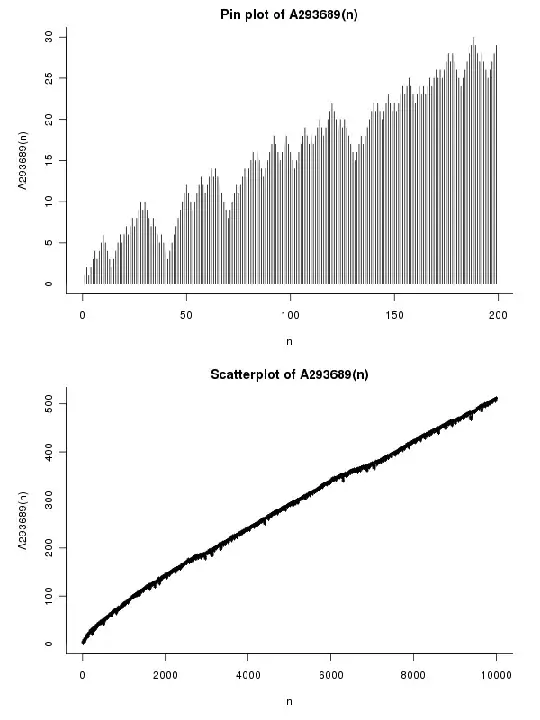
I have added this sequence to the On-Line Encylopedia of Integer Sequences (OEIS) as sequence A293689. Here's what the plot of the first 10000 terms looks like:

Code Golf Stack Exchange User Penguino said in a comment that $a(10^9) = 17156661$, and suggested that $a(n) \approx \frac{n}{\ln(n)\ln(\ln(n))}$. — Peter Kagey, Oct 24 '17 at 06:40

score 3 · Answer 1 · edited Sep 17 '19 at 13:58

I ran this for a while, and observed the following patterns:

First, the prime ant seems not to backtrack. The maximum that it can backtrack seems to be about $0.35\ln(x)+0.3$.

This sequence is the first number from which the ant backtracks a certain amount of steps (From 8, the ant backtracks all the way to 4 before going forward again, etc).

Value   Backtrack
4       1
8       4
12      7
35      14
200     15
357     17
486     18
675     19
1078    22
5726    23
8575    24
11373   25
15652   27
22660   28
24654   29
117672  33
455580  35
554340  37
801256  39
3362574 45

This can be strengthened by observing that given $S(n)$ as the first $n$ terms of the values left behind, there exists a value $x$ such that if $x$ is appended to $S(n)$, an ant placed on the sequence will backtrack before the start. Let $X(n)$ be the minimum of all numbers that could cause this for the first $n$ terms of the values the prime ant leaves behind. Then $X(n)$ eventually grows very rapidly, and the prime ant's sequence is well-defined.

Second, there seems to be little chance that anything greater than 7 will be left behind or that 7s will stop being left behind. The percentages barely change over time.

    9967 steps      6379946 steps
2   3248    32.59%  2183592 34.23%
3   2212    22.19%  1373594 21.53%
5   2983    29.93%  1898510 29.76%
7   1524    15.29%  924250  14.49%

This is unsurprising, as once a number reaches 7 or lower, it needs to have a prime greater than 7 added to it in order to leave behind a prime larger than 7. I don't know how to formalize it, though. We could probably make a pretty good heuristic argument.

Does the "prime ant" ever backtrack?

1 Answers1