41

What is the height of the red bar?

the problem

My try: with respect to the picture, it seems for the green bar $\frac{h}{H}=\frac{2}{3}$. So, I think that ratio is the same for the red bar, and the height of the red bar is $$\frac{h}{6+4}=\frac 23\qquad\to\qquad h_{red}=\frac{20}{3}$$

Is this correct?

amWhy
  • 210,739
Khosrotash
  • 25,772
  • I'm pretty sure this is a duplicate. I recall answering or commenting-on (or, at least, intending to) an identical question some time ago, but I can't seem to find it at the moment. – Blue Oct 13 '17 at 23:18
  • @Blue I agree. This one should be left because includes an explanation of a personal attempt. – gen-ℤ ready to perish Oct 14 '17 at 04:13
  • 4
    A sanity check you can make for yourself: are all the lengths that you are adding together (namely, the 6m and 4m lengths) pointing in the same direction? That is the property they must have for directly adding them to be the right operation. – Daniel Wagner Oct 14 '17 at 06:39
  • 1
    3 m of horizontal shadow corresponds to 2 m in height. So the 6 m of horizontal shadow from the red bar corresponds to 4 m in height. The 4 m of vertical shadow however corresponds to 4 m in height (just a 1:1 correspondence), so the total height of the red bar is 4 m + 4 m = 8 m. – md2perpe Oct 14 '17 at 06:39
  • 7
    For the dupe voter, I hope they don't close it as a dupe of that question because it has considerably lower quality than this one... don't close as dupe just because there's an older one, but close as dupe if there's a better alternative. (if possible, that question should be closed as a dupe to this one) – Andrew T. Oct 14 '17 at 12:12
  • 18
    I do not want to sound disrespectful, but is this a real question by the OP? It seems improbable to me that a PhD candidate in a Mathematics dept would be duped by this question. I am honestly puzzled. Am I missing something? – Thanassis Oct 15 '17 at 03:16
  • 1
    Why are we deleting this question? This question is better than the duplicate target. If anything we should close the other question as a duplicate of this one. – Matt Samuel Jun 06 '20 at 21:15

12 Answers12

116

Here is a different visualization. Shadow visualization

ayane_m
  • 157
Doug M
  • 58,694
  • 26
    +1. A picture is worth a thousand words (or $140$ characters of MathJax, at current exchange rates). – Brian Tung Oct 13 '17 at 21:59
  • 10
    Is there an implicit assumption that the light source is far away? It looks like that is the assumption that would make these slanted lines parallel. – Zach Boyd Oct 14 '17 at 06:36
  • 22
    @ZachBoyd a) It is the only assumption that makes the problem statement tractable. b) There is also the unstated assumption that the bars and the walls are vertical, and that the floor is horizontal, and that the dark areas are shadows and not some painting, and much more – Hagen von Eitzen Oct 14 '17 at 09:17
  • This was my initial intuitive guess, but then I realised that that the shadow on the back wall is not necessarily $1:1$. If the light is close then the shadow could be bigger than expected. – ctrl-alt-delor Oct 14 '17 at 10:12
  • 2
    So the picture isn't drawn to scale? The red bar doesn't look 4 times the height of the green bar. – camden_kid Oct 14 '17 at 10:12
  • 1
    They are never drawn to scale. if they were, then every geometry question would be a measurement question. – ctrl-alt-delor Oct 14 '17 at 10:13
  • 1
    @ctrl-alt-delor Wouldn't you have to prove it though rather than use measurements? – camden_kid Oct 14 '17 at 10:15
  • Having these questions, that can only be answered by solving “What must be assumed to make this question make sense”, are causing people to do engineering wrong. – ctrl-alt-delor Oct 14 '17 at 10:16
  • Doesn't the depth of the tower come into it? The light hits the front of the tower but the shadow measurement starts from the back this would mean that the 2m height equates to a shadow of length 3m + depth of the tower, which means the second 2m height would add more than 3m. – Lio Elbammalf Oct 14 '17 at 11:32
  • 2
    @LioElbammalf The light also falls on the top of the tower, and the far end of the shadow on the ground is cast by the rear of the top of the tower. In the picture above, the vertical lines are all on the back faces of the towers; if you also draw the front faces, they will be further to the left on the figure. – David K Oct 14 '17 at 19:03
  • 1
    @HagenvonEitzen we assume that the light source is far away not because the problem can't be solved otherwise but because the shadows of long red bar and the short green bar are parallel. – miracle173 Oct 14 '17 at 19:56
  • 6
    @ctrl-alt-delor All questions can only be answered by first assuming things that make the question make sense. For starters, you assume that the question is asked in English, that it has intended meaning, etc. – Joker_vD Oct 15 '17 at 01:16
31

3D histograms are evil according to Edward Tufte. Here, they are used to obfuscate information and make this geometry problem harder than it is. Also, as mentioned by @CandiedOrange and @LamarLatrell, the original drawing isn't to scale.

Here's a 3D render with correct heights:

enter image description here

By playing with perspective and point of view, you can seamlessly merge lengths that appear on distinct axes. It might give you the wrong impression that you could simply add those lengths.

from above

But if you select the correct perspective, the problem becomes much clearer.

enter image description here

enter image description here

Eric Duminil
  • 3,572
  • This is now the kickass answer. +1 – Lamar Latrell Oct 18 '17 at 09:19
  • 1
    This is some impressive visualization work. Any of these would improve the test over using the original image. – candied_orange Oct 18 '17 at 16:52
  • Late comment: I think 3D histograms aren't inherently evil, and have their place, but it's certainly true that their use is fraught with peril. – Brian Tung Jun 20 '20 at 18:24
  • @BrianTung. Do you have a good example? It'd be interesting to see if there are better alternatives. – Eric Duminil Jun 20 '20 at 20:06
  • @EricDuminil: I don't have a specific example at hand. I'm just saying that I've seen some that were helpful. I do recall that it depended on how the different categories were related. – Brian Tung Jun 20 '20 at 20:12
  • I think the problem can be solved by splitting the red bar into two parts ( 4m that gives 6m shadow and x that gives the 4m) now, draw a line to complete the rectangle 4x6. And a line from top of the red bar to the edge of the rectangle. You got a right triangle and using the sin rule of the right triangle, you get x = 6/sqrt(3) and the red bar height is 7.464 approximately – Monah Sep 13 '20 at 23:21
  • @Monah: Sorry, but this cannot be correct. 4m gives 6m horizontal shadow, and 4m gives 4m vertical shadow. Your x is 4m, not $\frac{6}{\sqrt3}$m, and the red bar is exactly 8m high. – Eric Duminil Sep 22 '20 at 13:12
  • @EricDuminil I would like to bring to your kind attention the fact that you cannot deal with the rays as parallel lines, if you draw lines from the source to the edges, you will get similar triangles, taking into consideration the light scattering as well. So, mapping 4m to 4m vertical works visually and not in mathematics in my opinion. – Monah Sep 23 '20 at 21:03
  • @Monah it seems to be the assertion, here, that the light source is at an infinite distance. Which would mean the rays are parallel. The problem cannot be solved otherwise, as far as I can tell. Every other answer seems to agree. If you don't, please feel free to add an answer with the corresponding drawing. I'm not sure I understand how your triangles would look like, or how you would solve for the unknown distance to the light source. – Eric Duminil Sep 24 '20 at 03:09
  • @EricDuminil I wonder what software did you use to create these graphics? – Jimmy Yang Nov 29 '20 at 02:39
  • 1
    @JimmyYang SketchUp. I described a similar animation here : https://math.stackexchange.com/questions/2550096/matrix-determinant-contradicts-corresponding-box-volume-how-is-it-possible/2551073#comment5268099_2551073 – Eric Duminil Nov 29 '20 at 06:25
15

There are three similar right triangles here and the ratios of their catheti (or legs) are all equal: $$\frac 23=\frac{4}{x}=\frac{h}{6+x} \implies x=6,\quad h=\frac{2(6+x)}{3}=8$$ ($x$ is the an imaginary cathetus which goes beyond the blue wall).

Robert Z
  • 147,345
13

The floor shadow is twice as long, and anything above that is reflective of the actual height (the bar and the wall are parallel, so their angle with the light source is the same). So, the red bar is twice the green bar $+ \ 4$ meters, which is $2\cdot2+4=8$ meters.

Alex Jones
  • 10,028
  • 1
    +1 the accepted answer is a visual representation of the same logic. – Gaurang Tandon Oct 15 '17 at 13:06
  • +1 for actually explaining what the accepted answer depicts (specifically the reasoning for why the vertical components have identical length). This is the key point and a vital missing link for anyone who didn't already understand it. – brichins Oct 16 '17 at 18:55
6

Basic approach. The $2$-meter green bar has a shadow of $3$ meters. It is $6$ meters from the red bar to the wall—how tall would it have to be for its shadow to extend right up to the foot of the wall? Call that height $h$.

How much taller would a bar have to be for the shadow to go up, vertically, another $4$ meters? That plus $h$ is your answer.

Brian Tung
  • 35,584
4

Suppose we had a third bar $2$m high that was at a distance $0.01$m from the back wall. All but $0.01$m of the shadow of that third bar would be on the wall, and the shadow on the wall could not be higher than the bar (because the light is shining at a downward angle), so it must be less than $2$m tall.

So the total length of shadow of the third bar is less than $2.01$m.

Your claim is that a bar's height is $\frac23$ the total length of its shadow on the ground and back wall combined. So you predict a height of less than $\frac23 (2.01)\mathrm m = 1.34\mathrm m.$

That is clearly not the height of the third bar.

Think again about your model. It may help to ask where you should put a notch in the taller bar so that the shadow of the notch is exactly at the corner where the ground shadow meets the back-wall shadow. Then figure how far is that notch from the top of the bar, and how far from the bottom.

David K
  • 108,155
4

Using similar triangles, we have $\dfrac{h_\text{red}-4}6=\dfrac23$, yielding $h_\text{red}=8$.

user1551
  • 149,263
3

As Zach Boyd mentions, this problem can only be solved if we assume that the light source is sufficiently distant (eg the sun) so that the light rays are parallel. miracle173 mentions that it looks like the light source is far away because the shadows of the two bars are parallel, but of course that could simply be a diagram artifact.

We also need to assume that the bars and back wall are vertical, and hence perpendicular to the floor (or if they aren't vertical they are at least parallel to each other)

So let's assume that the light rays are parallel, that the floor is horizontal, and that the bars and back wall are vertical. In which case, the lines connecting any object point to its corresponding shadow point are parallel. In particular, the lines from the tops of the bars to their shadow are parallel, so we have two key similar right triangles.

The key triangle of the green bar has a base of 3m and height of 2m. The key triangle of the red bar has a base of 6m and since it's similar to the green key triangle it has a height of 4m since $\frac{3}{2} = \frac{6}{4}$. That height is measured above the top of the shadow of the red bar (as illustrated in the diagram in Doug M's excellent answer). The top of the shadow of the red bar is 4m above floor level, thus the total height of the red bar is 8m.

PM 2Ring
  • 5,544
3

The vertical bar height is$ \frac23$ length of its uninturrupted shadow length. So $ \dfrac23 \cdot 6 =4.$

Rest of the red bar casts s a direct $1:1$ vertical projection/translation of $4$ length onto the wall. So red height total height of red bar is $4+4=8.$

Else symbolically

$$ h-4 = \frac23 \cdot 6 \, \rightarrow h= 8. $$

Narasimham
  • 42,260
3

Without doing any real math it's fairly simple to determine that the red bar is 8 meters tall.

Rationale: The 2m green bar casts a 3m shadow, so it would take a 4m bar to cast the 6m shadow between the red bar and the wall, and thus the lower portion of the red bar is 4m tall. The red bar is parallel to the wall, so the 4m shadow on the wall is cast by the upper 4m of the bar. 4m + 4m = 8m, so the bar is 8 meters tall.

Bob Jarvis - Слава Україні
  • 135
2

This image is flawed. At least if those black bars are shadows some one has been playing with the lighting.

If the red bar is meant to be 8m (and I think it is) it should look like this:

enter image description here

Instead it looks like this:

enter image description here

Which I can prove is not 8m by arguing that the 4m mark is halfway up the blue wall. That means the blue wall is 8m and a 8m red bar should be no taller than the blue wall. Yet it is taller, as the yellow box shows.

The red bar given is somewhere between 11-12m. Sure, that isn't what the person who drew this was thinking. But this is a terrible inconsistency to confront students with. This isn't math. This is "guess what I'm thinking".

Now sure, this assumes the image is drawn in a particular 3D style. But it's one that mathematics students are familiar with. Can you guess which one?

enter image description here

The essential assumption is that lines that are parallel in 2D are parallel in 3D.

candied_orange
  • 712
  • 2
    The drawing is only here to show the concept and the assumptions. It isn't to scale probably to prevent the reader from simply guessing or measuring the height. It's actually pretty common in math : The alpha angle in this triangle could be any value between 0° and 180°. There's no need to take every drawing literally. – Eric Duminil Oct 17 '17 at 17:56
  • @EricDuminil sorry but that's just "guess what I'm thinking" talk. Real math doesn't care how you solve it. If you only want it solved one way say what way. – candied_orange Oct 18 '17 at 02:14
  • 2
    Since it's a math problem, you might want to trust and use the numbers ;) – Eric Duminil Oct 18 '17 at 06:32
  • @EricDuminil there are at least 3 ways to solve this problem. They all use "the numbers". The sad thing is they give three different answers. You're picking one only because it uses the most numbers. That's just a test taking skill. One you shouldn't be punished for not having in a math test. – candied_orange Oct 18 '17 at 12:54
  • 1
    Interesting. What are the other ways? Wouldn't it make sense to use all the provided numbers? BTW, I've updated my answer to show what a correct 3D diagram would look like. – Eric Duminil Oct 18 '17 at 12:57
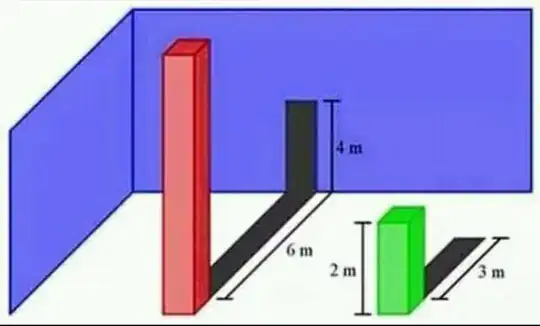
  • @EricDuminil All these ways use numbers. Others have shown how to get 8m. Above I show how to get 11-12m. You can also get 5-6m by measuring the red bar as a little under 3 green bars. The green bar should be no further back then the red bar so claiming this is simply "not to scale" really doesn't fix it. All the ways to solve the problem should agree. Otherwise we're just looking at abstract art. There simply isn't anywhere to stand where a 3D construct would produce this 2D image if we assume right angles here. Asking students to sort through that nonsense on a math test is simply wrong. – candied_orange Oct 18 '17 at 14:38
  • 1
    Have you taken note that most other answers seem to use the numbers quite naturally? In my opinion it is because of the core reason that they are the only set of information presented that isn't unambiguous. Your answer is helpful in that it points out the rest, but that doesn't mean that the numbers are necessarily wrong. As @EricDuminil has said " It isn't to scale probably to prevent the reader from simply guessing or measuring the height". – Lamar Latrell Oct 20 '17 at 06:20
  • Thanks for showing what "oblique" is. I didn't know it, and had a hard time getting the same perspective in Sketchup than in the original drawing. Now I know why! – Eric Duminil Oct 20 '17 at 06:34
  • @LamarLatrell the problem is that for some people trusting only one way to solve it over the others isn't natural. Questions like this unfairly penalize those people. Rather than a math test this acts more like a bad IQ test that unfairly selects for people who think the same way. There are better ways to avoid the alternate solutions. Simply stating what how it's meant to be solved is one. Not running the wall down the left side pointlessly is another. The green bar doesn't have to be placed in line with the red bar. You can't just say it isn't to scale because we NEED scale to solve it. – candied_orange Oct 20 '17 at 11:32
  • @EricDuminil Most welcome. Oblique is a style that actually distorts the image. But it follows certain rules. The issue here is those rules weren't followed. That penalizes those who know what the oblique rules are. If we don't follow something like that this turns into nothing but a 2D drawing. – candied_orange Oct 20 '17 at 11:36
  • There is more than one way to interpret the image using cues from the image right? If so, then that approach is ambiguous and the answer would/could be 'I see 2 (or more) answers and here is the logic behind them...' . But in using the numbers, I personally can only see a singular and unambiguous answer (8m). To my mind that is a more secure assumption, or put another way, it's what a reasonable (and yes, numerate) person would offer as a solution in a contextless situation. – Lamar Latrell Oct 20 '17 at 13:54
  • @LamarLatrell and so long as you refuse to see it any other way you'll have no idea why you're failing smart talented students who can see more than you do. – candied_orange Oct 20 '17 at 15:36
  • I see what you're saying (at least I think I do??). I'm saying that ... well, I'm saying what I've already said.. (!) I'm wondering if you've carefully read my comments? Maybe I'm not being clear enough? Question: if the image was a photo of actual properly scaled objects with the correct heights and the measurements overlaid would you be just as critical and request that the focal length, sensor size, distance between the camera and the objects etc. were also given as information? Or would you then simply use the logic that the other 7 or 8 answers have done? – Lamar Latrell Oct 20 '17 at 20:10
  • @LamarLatrell The trap is that the question appears objective when it's not. Those that fail to see it as subjective and were lucky enough to pick the correct way to solve it can easily feel the solution is obvious when it's not. I've proven the other ways and you're still assuming the problem is me. I even showed how to correct the problem and you still think it's me. That's the problem with the game of "guess what I'm thinking". – candied_orange Oct 20 '17 at 20:35
  • Thanks for confirming you're not actually reading my comments. Big hug and pat on the back + laters ;) – Lamar Latrell Oct 21 '17 at 06:21
  • Let us continue this discussion in chat. – candied_orange Oct 21 '17 at 12:51
1

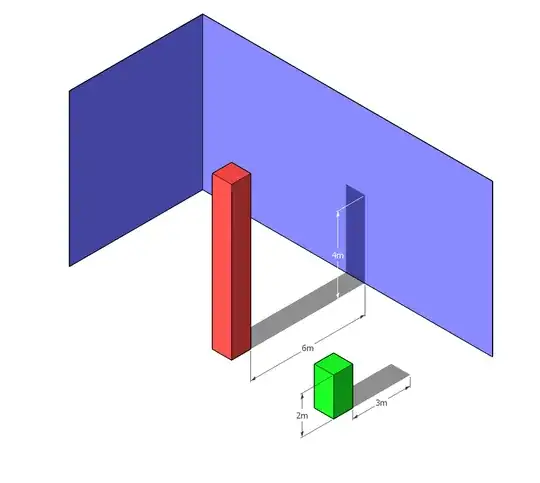
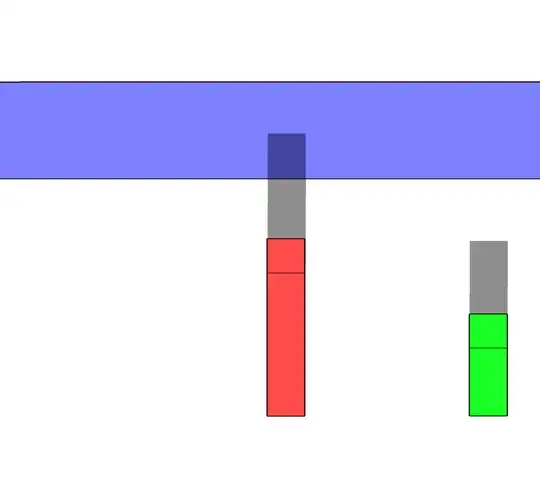
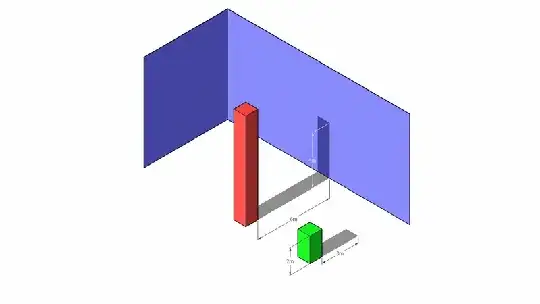
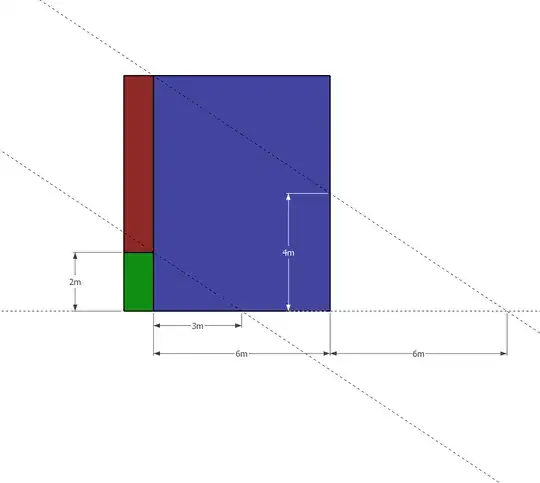
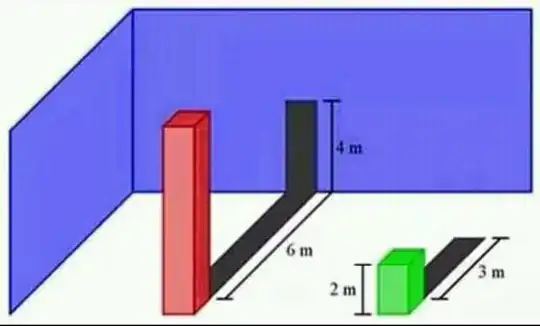
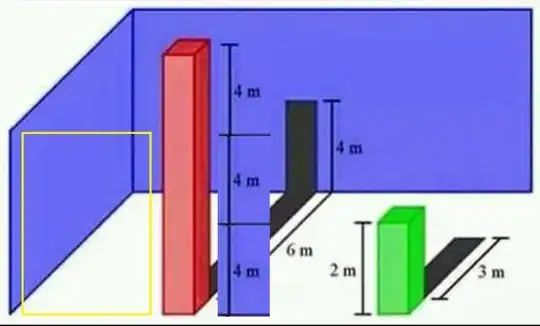
Visualising the model is a bit tricky. The eye cannot see the tiny differences. One of the great examples that eyes can be trapped is the missing square puzzle. Therefore, we cannot rely on the visual presentation of the model to calculate the height.

Here, I will try to present the problem mathematically:

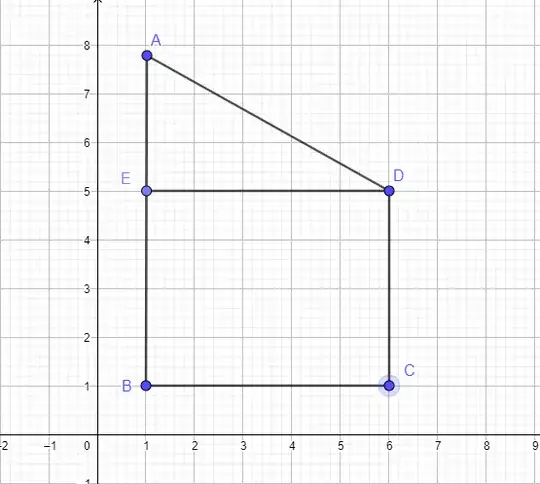
enter image description here

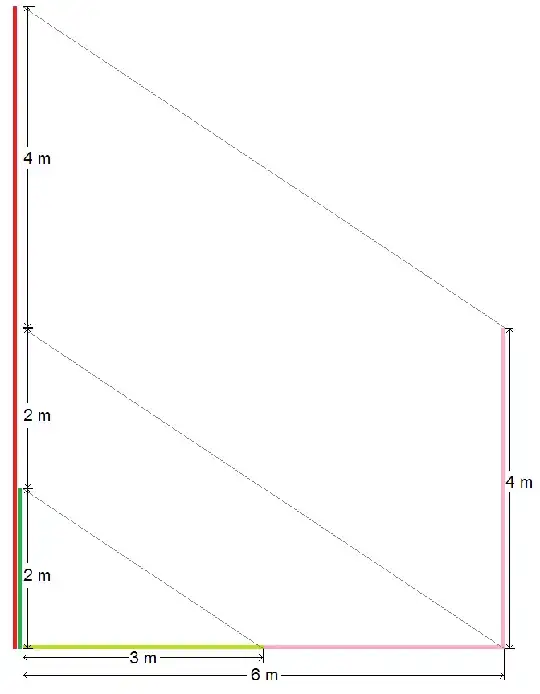
We know the length of $BC=6m$ which represents the horizontal shadow, $CD=4m$ which represents the vertical shadow, $BE=4m$, $AE=x$

height of the red bar is $AE + BE = 4m + x$

$\angle{AED}=90^\circ$ and $\angle{ADE}=60^\circ$ and $\angle{ADE}=30^\circ$

So, $AD=2x$ and $ED=x\sqrt{3}=6m \Rightarrow x = \frac{6}{\sqrt{3}}$

$AB = 4m + \frac{6}{\sqrt{3}}m \approx 7.464m$

Monah
  • 123
  • 6