I used classical ($4^\text{th}$ order) Runge-Kutta method to solve the ODE $$y'=5e^{5t}(y-t)^2+1,0\leq t\leq 1, \ y(0)=-1.$$
$h$ is the step size.
When $h=0.2$, I got a good approximation of the solution. However, when $h=0.25$, the result went to infinity. What's the reason for this? What's restriction of the step size and convergent condition for classical RK method?
The exact solution is contained in the box $(t,y(t))\in[0,1]\times[-1,1]$. Using a bound on the $y$ derivative as Lipschitz constant and using $y'\ge 1\implies y(t)>t+y(0)$ gives $L=10e^5=1484.13..$. A simplified stability condition for RK4 is $Lh\le 2.5$, which all the discussed step sizes do not satisfy. The Lipschitz constant can be improved using a non-rectangular region around the exact solution, however it is doubtful that one would get $L\sim 12$ which would be required to explain the qualitatively good behavior of $h=0.2$. However, that one observes grossly deviating behavior for such large step sizes as in $h=0.25$ is not surprising.
Set $u(t)=\frac1{y(t)-t}$ then $u'(t)=-5e^{5t}$ so that $$ u(t)-u(0)=1-e^{5t} $$ Inserting $u(0)=\frac1{y(0)}$ gives the solution in the original variables $$ y(t)=t+\frac{y(0)}{1-y(0)(e^{5t}-1)}. $$ The denominator has a root at $t=\frac15\ln(1+\frac1{y(0)})<1$, so that $y$ has a pole inside the integration interval for $y(0)>\frac1{e^5-1}$.
The originally given wrong initial condition $y(0)=1$ would fall into this situation with a numerical position for the pole at $0.13862943611198905$, making steps with step sizes $h=0.2$ or $h=0.25$ meaningless. With step sizes $h<0.1$ this pole will be captured in some way. Due to the tendency of explicit methods to straighten convex solution curves is that the divergence will be reached later than in the exact solution, moving to the correct position with finer step sizes.
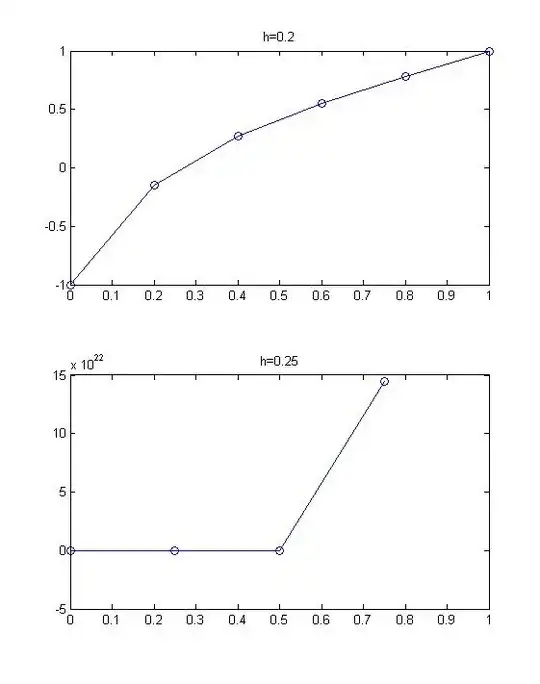
With the corrected initial condition $y(0)=-1$, then also $u(0)=-1$ the exact solution has the simple form $$y(t)=t-e^{-5t}.$$ The $y$-derivative of the ODE function along this path is $\max_{t\in[0,1]}|5e^{5t}\cdot2(-e^{-5})|=10$. If the step size is small enough so that the numerical solution stays close to the exact solution, the simplified stability condition gives $h<0.25$. However, any deviation from the exact solution has a positive feed-back effect in that the Lipschitz constant for the larger region rapidly increases, making the violation of the bound for admissible step sizes more acute, which is what happens at $h=0.25$ where at $t=0.5$ the computed value is $y=3.4375$ which is far away from the exact value $0.4179$ and has a derivative of $f(t,y)=526.5992$ giving dangerously large offsets in the stages of the next RK4 step.
Another view of this problem is to consider the exact solutions going through the points of the numerical method. If these exact solutions are not well-behaved in forward time, then also the numerical method can not be expected to give better results. In the following plot one sees that the situation is not very stable even for $h\in[0.1,0.2]$, where the numerical solution itself looks acceptable. The divergence for $h=0.25$ is present in the exact solutions with the point after the first step.
The equation is initially written in a somewhat misleading fashion. You should really look at $z(t)=y(t)-t$ and notice
$$\frac{dz}{dt}=5e^{5t}z^2,z(0)=-1.$$
The real solution to this problem is going to try to make its way up to zero and then stabilize there. Indeed you can actually calculate that $z(t)=-e^{-5t}$ which shows that.
But a numerical solution, especially with an explicit method, will tend to overshoot $z=0$. Then the $z^2$ term triggers finite time blowup, just like in the exact solution to $z'=5e^{5t}z^2,z(0)=z_0>0$. This overshoot problem is the same as the problem that happens in $y'=\lambda y$ where the equilibrium $y=0$ solution is overshot by explicit methods with too large of step sizes.
To put it another way, what you are seeing is the dramatic difference in behavior between $y'=y^2,y(0)=-1$ and $y'=y^2+\varepsilon,y(0)=-1$ which occurs for any $\varepsilon>0$. This is an intrinsic instability in the equation which creates difficulties in the numerical solution.
