1

I have two functions: $ u(x) $ and $ v(x) $.

I have another function: $ f(u, v) $.

I want to find: $ \frac{\operatorname df}{\operatorname dx}$.

Is there a rule that goes like this?

$$ \frac{\operatorname df}{\operatorname dx} = \frac{\partial f}{\partial u} \cdot \frac{\operatorname du}{\operatorname dx} + \frac{\partial f}{\partial v} \cdot \frac{\operatorname dv}{\operatorname dx} $$

If yes, what is this rule called and how can I prove this relationship?

If no, what is the correct rule to compute what I want?

Math Learner
  • 1,113
  • 4
    Yes. It's called the chain rule. – Vim Sep 05 '17 at 02:25
  • Be aware that the notation style you are using, while common, is rather inconsistent and ambiguous, which may be obscuring your understanding. For example, given the actual setting, because the four variables $f,u,v,x$ are all pairwise dependent, you should actually have $\partial f/\partial u = \mathrm{d}f/\mathrm{d}u$, and equations $$ \frac{\mathrm{d}f}{\mathrm{d}x} = \frac{\mathrm{d}u}{\mathrm{d}x} \frac{\mathrm{d}f}{\mathrm{d}u} = \frac{\mathrm{d}v}{\mathrm{d}x}\frac{\mathrm{d}f}{\mathrm{d}v}$$ Of course, nobody actually means that. –  Sep 05 '17 at 03:20
  • @Hurkyl Did you mean the following instead? $$ \frac{\operatorname df}{\operatorname dx} = \frac{\operatorname du}{\operatorname dx} \frac{\operatorname df}{\operatorname du} + \frac{\operatorname dv}{\operatorname dx} \frac{\operatorname df}{\operatorname dx} $$ You have used an additional $=$ sign instead of $+$ sign and I am confused if that is correct. – Math Learner Sep 05 '17 at 04:23
  • @Lone: Nope, I actually meant what I wrote! This is just one of many examples why I think $\partial f / \partial u$ notation is terrible. More often than not, it means "fill in here the thing I actually mean, not what I wrote". And I don't think I'm even exaggerating! –  Sep 05 '17 at 04:24
  • @Hurkly Thanks for the clarification. You are right indeed. We can always express $ v $ in terms of $ u $ or vice-versa and work with the single-variable chain rule. – Math Learner Sep 05 '17 at 04:38

1 Answers1

1

Quick note, here is the proper statement and a good proof of the chain rule if that's what you wished to find.

As Vim pointed out in your comments, this is the chain rule. I've always thought of it like a tree which may help you grasp it faster.

For instance, consider the function $F\bigg(x\big(u(t),v(t)\big),y,z(t)\bigg)$. This corresponds to the following tree:

1111

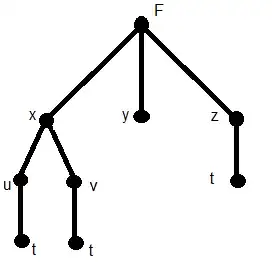
As you see, the child of every vertex represents its "input". Perhaps you want to find $\dfrac{dF}{dt}$. You start at the root $F$ then move over edges to your goal of $t$. Now notice our goal appears multiple times in this tree, so the paths we could take are:

$$\begin{cases} \ F \to x \to u \to t \\ \ F \to x \to v \to t \\ \ F \to z \to t \end{cases}$$

Now, consider just the first case above of $$F \to x \to u \to t.$$ If the vertex you're "on" has more than one child, write it as a partial of the vertex you're on with respect to the vertex you're going to. If it has only one child, then don't use partials. Lastly, multiply all the steps together.

So for instance, our first step is $F \to x$. The vertex $F$ has more than one child, so we write $\dfrac{\partial F}{\partial x}$. Followed by $x \to u$ which provides $\dfrac{\partial x}{\partial u}$. Lastly, the step $u \to t$ is notated as $\dfrac{d u}{d t}$. All in all, for the first case we obtain $$\dfrac{\partial F}{\partial x} \dfrac{\partial x}{\partial u} \dfrac{d u}{d t}.$$

Now, since we're doing $\dfrac{dF}{dt}$, if that was the only vertex $t$ we would be done and $\dfrac{dF}{dt}$ would be the expression above. But there's two more cases, so let's do those. I expect you see the pattern, so here they are immediately:

$$\dfrac{\partial F}{\partial x} \dfrac{\partial x}{\partial v} \dfrac{d v}{d t}$$

$$\dfrac{\partial F}{\partial z} \dfrac{d z}{d t}$$

The very final step is to add our cases together. So we have the following:

$$\dfrac{dF}{dt} = \dfrac{\partial F}{\partial x} \dfrac{\partial x}{\partial u} \dfrac{d u}{d t} + \dfrac{\partial F}{\partial x} \dfrac{\partial x}{\partial v} \dfrac{d v}{d t} + \dfrac{\partial F}{\partial z} \dfrac{d z}{d t}.$$

Andrew Tawfeek
  • 2,654