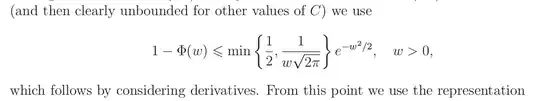0

In the notes Fundamentals of Stein’s method in page 7 one reads

enter image description here

here $\phi(x) = \int_{-\infty}^x \frac{1}{\sqrt{2\pi}}e^{-t^2/2}\, dt$

I would like to see first that $[1 - \phi(w)] \leq \frac{1}{2}e^{-w^2/2}$ for $w >0$ So since $\phi(0) = 1/2$ we have $1 - \phi(0) =\frac{1}{2}e^{-0^2/2} $, now taking derivatives

$$ \frac{d}{dw}[1 - \phi(w)] = - \frac{1}{\sqrt{2\pi}}e^{-w^2/2} $$ and

$$\frac{d}{dw}\frac{1}{2}e^{-w^2/2} = \frac{-w}{2}e^{-w^2/2}$$

So $$\frac{d}{dw}\big[\frac{1}{2}e^{-w^2/2}\big] -\frac{d}{dw}[1 - \phi(w)] = \bigg(\frac{1}{\sqrt{2\pi}} - \frac{w}{2}\bigg) e^{-w^2/2} $$

which is negative for $w > \frac{2}{\sqrt{2\pi}}$. In this case, it may be that $$\frac{1}{2}e^{-w^2/2} <[1 - \phi(w)] $$

How do I see that this is not the case?

Now, consider the next inequality implied by the display in the figure:

$$ [1 - \phi(w)] \leq \frac{1}{w\sqrt{2\pi}}e^{-w^2/2}$$

At $0$ the right hand side is $\infty$. checking the derivatives now we see

$$\frac{d}{dw}\big[\frac{1}{w\sqrt{2\pi}}e^{-w^2/2}\big] =-\frac{1}{\sqrt{2\pi}}e^{-w^2/2} - \frac{1}{w^2\sqrt{2\pi}}e^{-w^2/2} $$ and so

$$ \frac{d}{dw}\big[\frac{1}{w\sqrt{2\pi}}e^{-w^2/2}\big] -\frac{d}{dw}[1 - \phi(w)] = - \frac{1}{w^2\sqrt{2\pi}}e^{-w^2/2} $$

which is negative so It is also not clear that

$$ [1 - \phi(w)] \leq \frac{1}{w\sqrt{2\pi}}e^{-w^2/2}$$

Maybe the author meant

$$ [1 - \phi(w)] \leq \max\big\{\frac{1}{2},\frac{1}{w\sqrt{2\pi}}\big\}e^{-w^2/2}$$

Still it is not clear that the inequality will hold, since for $w \geq \frac{2}{\sqrt{2\pi}}$ the inequality we would like to hold is $$ [1 - \phi(w)] \leq \frac{1}{2}e^{-w^2/2} $$

which is from the derivative sign we see that $\frac{1}{2}e^{-w^2/2} - [1 - \phi(w)] $ is decreasing and we still need to check if this is always positive.

Any ideas?

Edit For the first bound and a simple argument using no derivatives see Normal distribution tail probability inequality

Conrado Costa
  • 6,239

1 Answers1

2

Note that for $x>0$:

$$1-\Phi(x)=\frac{1}{\sqrt{2\pi}}\int_x^{\infty}e^{-t^2/2}\,dt\leq \frac{1}{\sqrt{2\pi}}\int_x^{\infty}\frac{t}{x}e^{-t^2/2}\,dt=\frac{e^{-x^2/2}}{x\sqrt{2\pi}}$$

and that $1-\Phi(x)<\frac{1}{2}$ for every $x>0$, so the author meant what he wrote.

If one insists on using the derivative, then one may note that the inequality to prove is equivalent to this one: $$\Phi(x)+\frac{\Phi^{'}(x)}{x}\geq 1$$ Differentiating the function $g(x)=\Phi(x)+\frac{\Phi^{'}(x)}{x}$ one obtains: $$g'(x)=\frac{e^{-x^2/2}}{\sqrt{2\pi}}\left(1-\frac{x^2+1}{x^2}\right)$$ since $g'(x)<0$ for all $x>0$ and $\lim_{x\to\infty}g(x)=1$, one deduces, (by considering derivatives!) that $g(x)\geq 1$ for all $x>0$.

Evidently, the proof obtained by considering derivatives is somewhat longer and much less to the point than the concise inequality above.

uniquesolution
  • 18,982