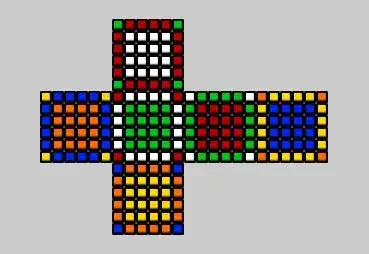
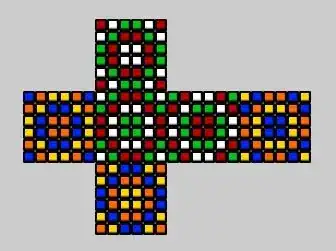
Suppose, Initial state Rubik's Cube 6x6x6
444444 444444 444444 444444 444444 444444 000000 111111 222222 333333 000000 111111 222222 333333 000000 111111 222222 333333 000000 111111 222222 333333 000000 111111 222222 333333 000000 111111 222222 333333 555555 555555 555555 555555 555555 555555
I want to find a final state using basic slice and face moves, where in each face 6x6 the columns and rows don't have repeating colors (numbers), for example:
0 2 3 4 5 1 1 5 0 2 4 3 5 0 4 3 1 2 2 3 5 1 0 4 4 1 2 5 3 0 3 4 1 0 2 5
I found a final state very close to the desired one (only one piece out of place) Using the following algorithm
bucket is rubik cube 6x6x6 empty
fill_board()
if length available positions is 0
return True
position = pop available positions
for each N in random.sample([0,1,2,3,4,5,6],6)
bucket[position.i][position.j] = N
if bucked is not valid
continue
if fill_board //Recursion call
return True
bucket[position.i][position.j] = None //backtracking
append position in available positions //backtracking
return False
Nearby state found:
015324 451230 120453 342501 203145 534012 320154 135042 315024 315240 254013 513420 420153 052134 413202 351204 153240 143502 ---- check first 2 045231 204153 531402 524013 102345 042315 042531 401325 531420 420531 204315 230451 042351 215403 153024 530142 421530 304215
My hypothesis is that there is no sudoku state for the rubik's cube 6x6x6, I am agricultural engineer and I do not know how to validate or refute it, with my algorithm if I find a sudoku state would refute it
Is there someone who can help me?