5

I have 2D point clouds which are 4-way symmetrical (invariant by 90° rotation). The points are usually arranged on the nodes of a square grid, densely populated, but some cases can be more complicated. I do know the point pattern in advance.

I need to find the symmetry axis, which are arbitrarily oriented. I initially thought of the moments of inertia, but in the case of symmetrical clouds the ellipse of inertia is a circle and no orientation information can be obtained.

In addition, the method should be robust because a few points (say <2%) can be missing, displaced or extraneous. There can be between 500 and 2500 points in total.

Any suggestion about how this can done efficiently ? I suspect that some other moments can do.

Typical case:

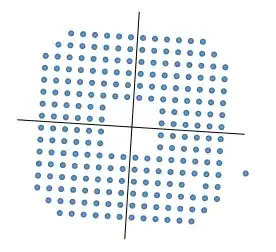
enter image description here

Rodrigo de Azevedo
  • 23,223
  • This may be useful: Robust principal axes determination for point-based shapes using least median of squares. – Rodrigo de Azevedo Jul 30 '17 at 12:40
  • What about taking a point at random and find its four closest neighbours, to see if they form a cross-like pattern? – Intelligenti pauca Jul 30 '17 at 17:23
  • @Aretino: this makes sense. In certain cases there will be complications because there can be several grids and/or irregularities so that not all points form a cross. –  Jul 30 '17 at 18:12
  • (1) Don't you have another set of symmetries 45 degrees rotated from your black 'axes'? (2) Have you investigated what happens to correlation as you rotate? – BruceET Jul 31 '17 at 03:25
  • Perhaps this link can give you some inspiration. Though the algorithm description isn't very clear, the source code has a lot of commentary. – Jens Jul 31 '17 at 16:26
  • For clarification, are we looking for axes with rotational symmetry or with reflectional symmetry? Could the point cloud be e.g. a swastika, which is invariant by $90^\circ$ rotation? – Jens Aug 02 '17 at 00:36
  • @Jens: reflectional. –  Aug 02 '17 at 06:23
  • I'd find the nearest neighbor vectors for all points, including all neighbors closer than $\sqrt{2}$ the distance to the closest neighbor for that point. If most of the points are in a regular lattice, say $K$ points of $N$ are in a regular lattice, then you only need to consider neighbors up to a distance $L$ where at least $K$ points have a neighbor at distance $L$ or closer. Since you know the number of points, and the rough density beforehand, the cell method can speed up the neighbor search to almost linear time. The neighbor vectors match lattice basic vectors, and thus orientation. – Nominal Animal Aug 05 '17 at 18:31
  • @NominalAnimal: the pattern maybe a combination of regular lattices and this approach might fail. Anyway as we know the pattern, maybe a histogram of distances/directions to the nearest neighbor can help. –  Aug 07 '17 at 06:21
  • @YvesDaoust: The histogram of directions sounds like a very robust approach, but it has very limited angular precision (bin width cannot be too small compared to number of vectors, or you cannot detect the peaks reliably). I think I'll look at applying a disjoint set data structure, either merging vectors $i$ and $j$ iff $\vec{v}_i \cdot \vec{v}_j \ge \beta \lVert \vec{v}_i \rVert \lVert \vec{v}_j \rVert$ with $\beta$ slightly less than 1; or by clustering the points first into separate lattices. Do you have any point clouds (non-rotated?) I could play with? – Nominal Animal Aug 07 '17 at 09:45

2 Answers2

2

A point cloud which is 4-way symmetrical will have 4 axes of reflectional symmetry, where each axis is offset from the next by 45 degrees. To find all axes it therefore suffices to find one.

The following home-made algorithm works pretty well at finding that axis. Trial testing of clouds with an average of 500 points gives the following statistics regarding the deviation $D$ between the axis angle found by the algorthm and the true axis angle:

Perfect cloud:

$D \lt 1^\circ$: $100$%

Cloud with 2% missing points:

$D \lt 1^\circ$: $55$%

$D \lt 2^\circ$: $90$%

$D \lt 3^\circ$: $99$%

I'll discuss problem areas at the end of the post, but first to the algorithm.

Algorithm overview

For a 4-way symmetrical cloud, at least one axis of symmetry must exist within any $45^\circ$ sector, as seen from the centroid of the cloud. At the extreme, there will be one axis at the very start of the sector and another axis at the very end of the sector. An axis of symmetry is characterised, in this case, by the fact that all points within a $45^\circ$ sector to the "left" of the axis are mirrored by the points within a $45^\circ$ sector to the "right" of the axis. A very simple (non-robust) way to check if an axis at a given angle is an axis of symmetry, is to see if the number of points in the $45^\circ$ sector to the left of the axis is equal to the number of points in the $45^\circ$ sector to the right of the axis. A better way (which this algorithm uses) is to check if the sum of the distances from the centroid to the points in the $45^\circ$ sector to the left of the axis, is equal to the sum of the distances to the points in the $45^\circ$ sector to the right of the axis.

So, the basic idea of the algorithm is to have an axis move from $91^\circ$ to $44^\circ$ in $1^\circ$ steps, calculating the sum of the distances to the points in the left sector and the sum of the distances to the right sector at each step, and comparing these sums. The angle of the axis where the sums are "most equal" is then the algorithm's axis of symmetry.

The reason for using $91^\circ$ and $44^\circ$ instead of $90^\circ$ and $45^\circ$ is to avoid rounding problems. In addition, I use sectors of $47^\circ$ (which means the left and right sector overlap) instead of sectors of $45^\circ$ to avoid problems with points which are at or close to the dividing line between the left and the right sector.

The above is obviuosly not a robust method in general, but for a cloud where 4-way symmetry is assumed, it works.

Algorithm with details

Assuming all points are in an array with Cartesian coordinates:

  1. Find the centroid $(X_c, Y_c)$ of the cloud.

  2. Find the polar coordinates of each point, using $(X_c, Y_c)$ as origo, and save the points which have an angle between $91 + 46 = 137$ degrees and $44 - 46 = -2$ degrees in a new array $NewA$.

  3. Sort $NewA$ according to angle, from largest to smallest.

  4. Run through the angles $A$ from $91^\circ$ down to $44^\circ$ in steps of $1^\circ$. At each angle, calculate the distance sum for points in the left sector (i.e. points with $ A - 1 \lt$ angle $\lt A + 46$) and compare with the distance sum for points in the right sector (i.e. points with $ A + 1 \lt$ angle $\lt A - 46$).

  5. The angle $A$ at which this comparison is closest to one, is the algorithm's axis of symmetry angle.

Areas for improvement

  1. The algorithm is sensitive to "error" in the coordinates of the centroid. When points are missing or displaced, the centroid is not at the ideal (correct) location.

  2. The algorithm is also somewhat sensitive to the 2% errors if they mainly occur in the first and second quadrant (where this algorithm's input comes from).

Not sure what to do about these points.

Jens
  • 5,786
  • Quite interesting approach, which I could summarize as rating the degree of symmetry around a rotating axis (correct me if I am wrong). I guess that there is no need to scan in constant increments, you can try all angles leading to a point (increasingly after the sort by angle). –  Aug 08 '17 at 19:57
  • That's correct. An improvement I've thought of is to let the rotating axis run through all 360 degrees, finding the angles of all 8 "spokes" of the 4 symmetry axes, and then calculating the best fit line through the 8 data points. This will increase the computation time but should also substantially increase the accuracy. – Jens Aug 08 '17 at 21:26
  • Alternatively, run through the 360 degrees and just find the angle with greatest symmetry. – Jens Aug 08 '17 at 21:32
0

This is not an answer, but an extended comment that might lead to a workable solution.

I did some experiments, generating histograms of $$\chi_{ij} = -\chi_{ji} = \frac{x_j - x_i}{\lvert x_j - x_i \rvert + \lvert y_j - y_i \rvert}$$ and $$\gamma_{ij} = -\gamma_{ji} = \frac{x_j - x_i}{\lvert x_j - x_i \rvert + \lvert y_j - y_i \rvert}$$ with each sample weighed by $$\omega_{ij} = \omega_{ji} = \frac{1}{(x_j - x_i)^2 + (y_j - y_i)^2}$$ from rotated and translated point clouds with four-way mirror symmetry, with up to 10% additional (non-symmetric) or missing points.

Note that for $$\theta_{ij} = \arctan\left(\frac{x_j - x_i}{y_j - y_i}\right)$$we have $$\theta_{ij} = \begin{cases} \arctan\left(\frac{1}{\chi_{ij}} - 1\right), & 0 \le \theta \lt \frac{\pi}{2} \\ \arctan\left(1 - \frac{1}{\chi_{ij}}\right), & -\frac{\pi}{2} \lt \theta \le 0 \end{cases}$$ and $$\theta_{ij} = \begin{cases} \arctan\left(\frac{\gamma_{ij}}{1 - \gamma_{ij}}\right), & 0 \lt \theta \le \frac{\pi}{2} \\ \arctan\left(\frac{\gamma_{ij}}{1 + \gamma_{ij}}\right), & -\frac{\pi}{2} \le \theta \lt 0 \end{cases}$$

For $N$ points, there are $N(N-1)/2$ unique $i , j$ pairs, and the above is computationally cheap to calculate, and is relatively easily vectorized, too; single-precision or fixed-point integer arithmetic suffices for the purposes of the histogram. Where $\arctan$ or $\operatorname{atan2}$ might be considered too slow, the above should be fast enough.

The reason I think this might lead to a workable solution, is that the histogram shows extremely clear spikes along the symmetry/mirror axes for random point clouds. (Because of the sign differences, you need to look at both to determine the actual symmetry axes.)

For some regular lattices, I saw more spikes (as one would expect), including dual spikes in certain cases, so this definitely needs further math work (either comprehensive numerical research of different point clouds, or analysis on how the four-way mirror symmetry causes the spikes seen in the angular histogram, if properly weighted by the distance) before I'd consider it a solution.

Nominal Animal
  • 9,551