10

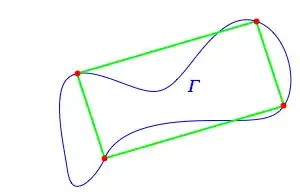
One of the most elegant demonstrations in topology is the proof of the inscribed rectangle problem (a solved variant of the unsolved inscribed square problem) which states that for any plain, closed continuous closed curve $\Gamma$ in $\mathbb{R}^2$, there exist four points that are the corners of an inscribed rectangle. (There are variants of this problem involving cyclicality as well.)

enter image description here

The proof relies on a clever representation of the locations of unordered pairs of points on $\Gamma$ with a point $p$ on a Möbius strip, and a function $f(p)$ that represents the Euclidean distance between the points on $\Gamma$.

The key step in the proof invokes the topological fact that the mapping of the Möbius strip and $f(p)$ to the plane of $\Gamma$, involving the unwrapping of the strip's boundary to coincide with $\Gamma$ guarantees that there exist two points, $p_1$ and $p_2$ that map to the same point on the plane and have the same value, i.e., $f(p_1) = f(p_2)$.

Is there a good reference, proof, or even intuitive demonstration of this fact?

Arnaud Mortier
  • 27,742
David G. Stork
  • 30,409
  • Are you sure the inscribed square problem is unsolved? – quasi Jul 20 '17 at 18:14
  • 1
    Yes I am (https://en.wikipedia.org/wiki/Inscribed_square_problem). – David G. Stork Jul 20 '17 at 18:16
  • In the January 1949 issue of the American Mathematical Monthly, on page 39, Orrin Frink proposed the problem: $$$$ Show that on every simple closed plane curve there are four points which are the vertices of a square. $$$$ In the June-July 1950 issue, on page 423, C.S. Ogilvy offered a proof. $$$$ So maybe without realizing it, Ogilvy assumed more than just a simple closed plane curve. – quasi Jul 20 '17 at 18:46
  • Yes... once you start putting on conditions (such as uniform convexity) then the problem has been solved. But for the general case... no. Interesting point, though: if there is an inscribed square (for general $\Gamma$) then there must be an odd (or infinite) number of them. Cool! – David G. Stork Jul 20 '17 at 18:49
  • 2
    This can be usefull I guess https://www.youtube.com/watch?v=AmgkSdhK4K8 – R.W Sep 29 '17 at 18:49
  • 1
    @RafaelWagner: Yes... that video was my introduction to this variant on the famous inscribed square problem. (I'm now a supporter through Patreon!) – David G. Stork Sep 29 '17 at 18:55
  • Really sorry i didn't clicked on it. But this is a great question in my view (+1) – R.W Sep 29 '17 at 18:57

3 Answers3

4

Just another version of Lao-tzu's answer. The mapping $f:M\to\mathbb R^3$ goes into the upper halfspace $z\ge0$ and the boundary $\partial M$ onto a curve $C$ in $z=0$. If injective, it is a homeomorphism onto its image $f(M)$ and $C$ is a Jordan curve. Thus, the interior $B$ of that Jordan curve is a disk, hence $N=f(M)\cup B\subset\mathbb R^3$ is the glueing of a Moebius band and a disk along their boundaries. Thus you have a projective plane $N$ embedded in $\mathbb R^3$. Contradiction.

Jesus RS
  • 4,551
  • Thanks that helps a bit, and a bit simpler than Lao-tzu's in that it apparently does not require the Klein bottle mapping theorem. – David G. Stork Oct 30 '19 at 23:38
  • In a sense, the non-embedding of the projective plane seems easier than that of the Klein bottle. But then, one uses the Schoenflies theorem, and that's why I only said "another version of Lao-tzu's answer". All in all this is a beautiful piece of topology worth any reworking – Jesus RS Nov 01 '19 at 09:16
  • I believe you mean embedded in $\Bbb R^3$ at the end. – Arnaud Mortier May 03 '20 at 07:44
  • Ammended! Thanks. – Jesus RS May 04 '20 at 08:28
3

Consider the geometric image of the given map $$\text{Möbius}\to \mathbb{R}^3$$ Suppose that there is no self-intersection point. Then by gluing an embedded disc along the boundary of the surface, below the plane $z=0$, one gets a connected closed surface embedded in $\mathbb{R}^3$. Such a surface has to be homeomorphic to $S_g$ for some $g$, by the classification of closed connected orientable surfaces and the fact that closed non-orientable surfaces won't embed in $\mathbb{R}^3$. It has Euler characteristic $2-2g$. Therefore with a disc removed it becomes $1-2g$, an odd number.

But the map above should induce a homeomorphism with the Möbius strip, which has Euler characteristic $0$.

Edit: A couple of attempts to build upon this proof in the case of finding a square:

  • Have the point "above" the middlepoint of each couple of points live in a fibre larger than just $\mathbb{R}$, so as to encode information regarding angles as well. For instance, the fibre could be $\mathbb{R}\times S^1$, with the second coordinate given by the angle $\mod \frac \pi 2$ between $\vec{AB}$ and a fixed direction. Problem of this approach: non-orientable surfaces do embed in four dimensions.
  • Study the set of self-intersection points of the above map. Try to prove that
    1. generically it should be an immersed $1$-submanifold whose boundary occurs when one side of the rectangle tends to have vanishing length: if that is the case, it is easy to see that it can't be the same pair of sides that vanish at both ends, therefore there has to be a square along the way.
    2. non-generic curves can be approached by generic curves and the squares in the latter tend to stay squares in the former.
Arnaud Mortier
  • 27,742
3

Here is a visable answer.

Let me denote the Möbius strip by $M$, with boundary circle by $\partial M$, then the Klein bottle is $K=M\coprod_{\partial M}M$. Let me also denote the two copies of $M$ inside $K$ by $M$ and $M'$. If the map $f: M\to\mathbb{R}^3$ in the video is injective in the interior $M\setminus\partial M$, then it's easy to see that $f: M\to\mathbb{R}^3$ is injective hence an embedding.

Moreover, it can be extended to a map $F: K\to\mathbb{R}^3$ in such a way that for $x\in M, x'\in M'$ which are "the same", we have $F(x)=-F(x')$ (or: this new big $F$ is the gluing of the small $f$ and $-f$, as $f|_{\partial M}=-f|_{\partial M}$ by construction). Then $F: K\to\mathbb{R}^3$ is an embedding. But it's well-known that the Klein bottle $K$ can't be embedded into $\mathbb{R}^3$.

Lao-tzu
  • 3,066