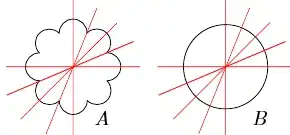
If we consider a curve with infinitely many distinct lines of reflectional symmetry, we generally think of a circle. However, can we prove that the circle is the only finite plane curve that has infinitely many lines of symmetry, or do more such curves exist? (I am not exactly certain of a formal term to describe this, but by "finite," I mean that the curve does not go to infinity at any point, i.e. for all $(x,y)$ on the curve, there exist some real numbers $a$, $b$, $c$, and $d$ such that $x\in[a,b]$ and $y\in[c,d]$; thus lines do not count as "finite" curves.)
So far, I have considered two possibilities for showing that circles alone have this property, but neither formally proves that circles are the only ones. The first is that finite plane curves with infinite reflectional symmetry will have a locus of points that are equidistant from some "center" (intersection point of two or more lines of symmetry), and I think that only a circle satisfies this property. The second is that a finite curve with any lines of reflectional symmetry can be divided into congruent parts by lines of symmetry:
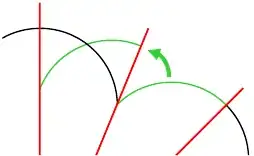
However, the pieces must be congruent no matter how many cuts are made in order for the curve to have reflectional symmetry. Therefore, the curve must possess infinite rotational symmetry too, because any "piece" (formed by the lines of symmetry) rotated onto any other piece must match. Otherwise, the pieces would intersect at a finite number of points. However, intersecting at a finite amount of points implies that another line of symmetry will cut the curve into non-congruent pieces, and thus it cannot have infinite reflectional symmetry. For example, we see curve A from earlier intersecting itself, showing that it does not have infinite rotational, and consequently reflectional, symmetry:
Only a circle, such as curve B, avoids such finite intersections.
Can either of these two demonstrations be formalized, or is there some other way to prove or disprove it? Any college-level answers are fine, but I would appreciate simpler answers.