A question on tangent line

Question

There is a curve $y=f(x)$ on the plane. Suppose that $M(x_0,y_0)$ is a point of the curve $y=f(x)$ and $f(x)$ is derivable at this point, i.e, there is a tangent line $L$ at this point.

Now there is another line $L'$ which is through $M(x_0,y_0)$ and the curve $y=f(x)$ is not on both sides of the line. See the picture.

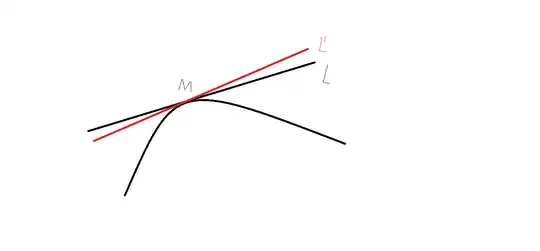Must $L=L'$ holds? I believe it is, but I cannot prove it. Could Someone help me?

First of all it is not necessary that curve remains on one side of the tangent line. Check the tangent to $y=x^{3}$ at origin. Next from your wording it looks like there is another line with a slope different from tangent. Then it will intersect the curve at some other point. — Paramanand Singh, May 26 '17 at 06:42
It won't necessarily intersect the curve in some other point. — Michael Hoppe, May 26 '17 at 08:20

Michael Hoppe · Accepted Answer · 2017-05-26T09:02:28.723

2

Let $y-y_0=m(x-x_0)$ be the equation of a line through $(x_0,y_0)$. Now that line lies only at one side of $f$ (in some neighborhood of $x_0$), so let wlog $y\geq f(x)$ except for $x_0$. From here: $$y_0+m(x-x_0)\geq f(x)\Rightarrow m(x-x_0)\geq f(x)-f(x_0).$$ If now $x>x_0$ it follows that $m\geq f'(x_0)$ and if $x<x_0$ we find that $m\leq f'(x_0)$.

edited May 26 '17 at 09:02

answered May 26 '17 at 08:39

Michael Hoppe

18,614

A question on tangent line

1 Answers1